Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo:
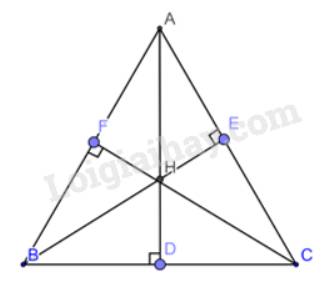
Xét tam giác BFC và tam giác BEC có :
BC chung
FC = BE
\(\widehat {BFC} = \widehat {BEC} = {90^o}\)
( cạnh huyền – cạnh góc vuông)
\( \Rightarrow \widehat C = \widehat B\) ( 2 góc tương ứng ) (1)
Xét tam giác CFA và tam giác ADC ta có :
CF = AD
AC chung
\(\widehat {ADC} = \widehat {AFC} = {90^o}\)
(cạnh huyền – cạnh góc vuông)
\( \Rightarrow \widehat C = \widehat A\)(2 góc tương ứng ) (2)
Từ (1) và (2) \( \Rightarrow \widehat C = \widehat A = \widehat B\) \( \Rightarrow \)Tam giác ABC là tam giác đều do có 3 góc bằng nhau

Giả sử tam giác ABC có các đường cao AH, BK, CI. Ta cần c/m AH, BK, CI đồng quy.
~~~~~~~
Qua 3 đỉnh A, B, C của tam giác, lần lượt kẻ các đường thẳng song song với các cạnh đối diện, chúng cắt nhau tại A'; B'; C'. (A' nằm khác phía với A qua BC, B' nằm khác phía với B qua AC, C' nằm khác phía với C qua AB).
Xét tam giác ABC và tam giác BAC' có:
góc BAC = góc ABC' (so le trong)
AB chung
góc ABC = góc BAC' (so le trong)
=> tam giác ABC = tam giác BAC' (gcg)
=> AC = BC'.
Chứng minh tương tự ta có AC = BA'.
=> BC' = BA' => B là trung điểm của A'C'.
Do BK _|_ AC, A'C' // AC => BK _|_ A'C'.
=> BK là đường trung trực của A'C'.
Cmtt => AH và CI là trung trực của B'C' và A'B'.
=> AH, BK, CI là 3 đường trung trực của tam giác A'B'C'. Ta dễ dàng c/m được 3 đường trung trực của tam giác đồng quy dựa vào tính chất điểm nằm trên đường trung trực của một đoạn thằng thì cách đều hai mút của đoạn thẳng đó. Vậy AH, BK, CI đồng quy tại 1 điểm, điểm đó gọi là trực tâm của tam giác ABC.

Ta có: ΔABC đều
mà AD,BE,CF là các đường trung tuyến
nên AD,BE,CF vừa là đường cao vừa là phân giác

Xét ΔAFC vuông tại F và ΔAEB vuông tại E có
CF=BE
góc ACF=gócABE
=>ΔAFC=ΔAEB
=>AC=AB
Xét ΔCEB vuông tại E và ΔCDA vuông tại D có
EB=DA
góc C chung
=>ΔCEB=ΔCDA
=>CB=CA=AB
=>ΔABC đều

a) Ta có tam giác ABC là tam giác đều,nên AB=AC=BC
Vậy các đường trung tuyến tương ứng cũng sẽ bằng nhau(AD=BE=CF)
b)Ta có tam giac ABC đều nên AB=BC,góc ABC=góc ACB
Xét tam giác ABD và tam giac ACD có
AB=AC(cmt)
góc ABC=góc ACB(cmt)
BD=CD(AD là đường trung tuyến)
VậyTam giác ABD=tam giác ACB(c-g-c)
Nên góc ADB=góc ADC
Ma 2 góc này bằng 180 độ
Mặt khác ta có tam giac ABD vuông tại D
Có AB=8cm
BD=4cm(BD=1/2BC.mà BC=AB)
Nên \(AB^2=AD^2+BD^2\)
\(8^2=AD^2+4^2\)
\(64=AD^2+16\)
\(AD^2=48\)
AD=\(\sqrt{48}\)
Xét Δ BEA và ΔCFA có:
BE = CF (gt)
BE ⊥ CA , CF ⊥ AB (vì BE, CF là đường cao Δ ABC) ⇒∠BEA = ∠CFA =900
Chung góc A, mà∠BEA = ∠CFA (cmt) ⇒ ∠ABE =∠ACF
⇒ Δ BAE = ΔCAF (g -c- g)
⇒AB = AC (2 cạnh tương ứng) (1)
Tương tự với Δ ECB , Δ DAC ta có: AC = CB ( 2)
Từ (1) , (2) ⇒ AB =AC =CB
⇒ Δ ABC đều
Bạn sử dụng định lý tam giác cân mà trả lời nhé! mk nhớ ko nhầm thì trong SBT có bạn nha!