
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(5x=3y\Rightarrow x=\dfrac{3y}{5}\)
Thay \(x=\dfrac{3y}{5}\) vào biểu thức \(x^2-y^2=-4\) ta có:
\(\left(\dfrac{3y}{5}\right)^2-y^2=-4\)
\(\dfrac{9y^2}{25}-y^2=-4\)
\(-\dfrac{16}{25}y^2=-4\)
\(y^2=-\dfrac{4}{\dfrac{-16}{25}}\)
\(y^2=\dfrac{25}{4}\)
\(\Rightarrow y=-\dfrac{5}{2};y=\dfrac{5}{2}\)
*) \(y=-\dfrac{5}{2}\Rightarrow x=\dfrac{3.\left(-\dfrac{5}{2}\right)}{5}=-\dfrac{3}{2}\)
*) \(y=\dfrac{5}{2}\Rightarrow x=\dfrac{3.\dfrac{5}{2}}{5}=\dfrac{3}{2}\)
Vậy ta được các cặp giá trị \(\left(x;y\right)\) thỏa mãn:
\(\left(-\dfrac{3}{2};-\dfrac{5}{2}\right);\left(\dfrac{3}{2};\dfrac{5}{2}\right)\)

Lời giải:
Áp dụng tính chất tổng 3 góc trong một tam giác bằng $180^0$
a.
$x=180^0-80^0-45^0=55^0$
b.
$y=180^0-30^0-90^0=60^0$
c.
$z=180^0-30^0-25^0=125^0$

Đổi 30 phút = 0,5 giờ
Quãng sông từ A đến B dài là:
\(x\) \(\times\) 0,5 + y \(\times\) 1 = 0,5\(x\) + y (km)
Kết luận Quãng đường từ A đên B dài: 0,5\(x\) + y (km)

Lời giải:
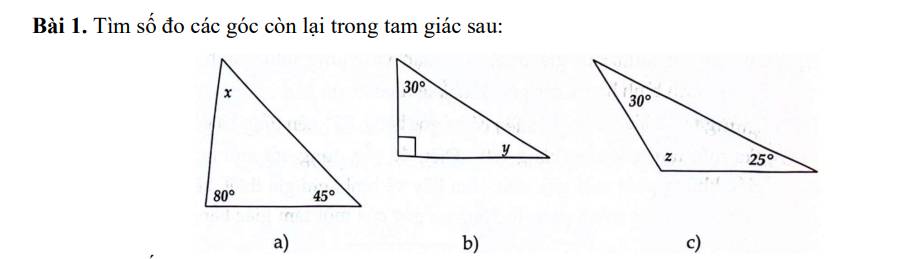
Áp dụng tính chất tổng 3 góc trong 1 tam giác bằng $180^0$
Hình 1: Hình không rõ ràng. Bạn xem lại.
Hình 2: $x+x+120^0=180^0$
$2x+120^0=180^0$
$2x=60^0$
$x=60^0:2=30^0$
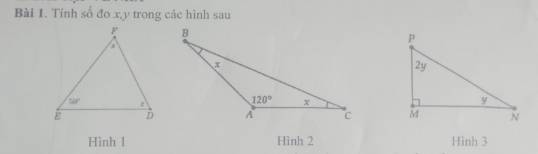
Hình 3:
$2y+y+90^0=180^0$
$3y=180^0-90^0=90^0$
$y=90^0:3=30^0$

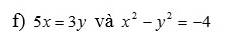


Bài 7:
p là số nguyên tố lớn hơn 3
=>p=3k+1 hoặc p=3k+2
Nếu p=3k+1 thì \(8p+1=8\left(3k+1\right)+1=24k+9=3\left(8k+3\right)⋮3\)
=>Loại
=>p=3k+2
\(4p+1=4\left(3k+2\right)+1=12k+9=3\left(4k+3\right)⋮3\)
=>4p+1 là hợp số
Bài 6:
a: TH1: p=3
p+2=3+2=5; p+4=3+4=7
=>Nhận
TH2: p=3k+1
p+2=3k+1+2=3k+3=3(k+1)
=>Loại
TH3: p=3k+2
p+4=3k+2+4=3k+6=3(k+2)
=>Loại
b: TH1: p=5
p+2=5+2=7; p+6=5+6=11; p+18=5+18=23; p+24=5+24=29
=>Nhận
TH2: p=5k+1
p+24=5k+1+24=5k+25=5(k+5)
=>Loại
TH3: p=5k+2
p+18=5k+2+18=5k+20=5(k+4)
=>Loại
TH4: p=5k+3
p+2=5k+3+2=5k+5=5(k+1)
=>Loại
TH5: p=5k+4
p+6=5k+4+6=5k+10=5(k+2)
=>Loại
Vậy: p=5
Bài 5:
Với p=2 => 7p+5=7*2 + 5 = 19 (tm)
Với p>3
TH1: p=3k+1
=> 7(3k+1)+5=21k+7+5=21k+12=3(7k+4) ⋮ 3
=> 7p+5 là hợp số
TH2: p=3k+2
=>7(3k+2)+5=21k+14+5=21k+19
Vì p là số nguyên tố lớn hơn 3 => p lẻ => 3k + 2 lẻ => 3k lẻ => k lẻ
k lẻ => 21k lẻ => 21k + 19 chẵn => 21k+19 ⋮ 2
=> 7p+5 là hơn số
Vậy có p=2 là thỏa mãn