K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2021
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
Tương tự: \(\left\{{}\begin{matrix}SA\perp CD\\AD\perp CD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\Rightarrow CD\perp SD\)
\(\left\{{}\begin{matrix}SA\perp BD\\AC\perp BD\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\Rightarrow\left(SBD\right)\perp\left(SAC\right)\)
b.
Do M, N là trung điểm SB, SD \(\Rightarrow\) MN là đường trung bình tam giác SBD
\(\Rightarrow MN||BD\)
Mà \(BD\perp\left(SAC\right)\) (cmt) \(\Rightarrow MN\perp\left(SAC\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2021
c.
K là trung điểm SA, M là trung điểm SB \(\Rightarrow KM\) là đường trung bình tam giác SAB
\(\Rightarrow KM||AB\)
Mà \(SA\perp\left(ABCD\right)\Rightarrow SA\perp AB\Rightarrow SA\perp KM\) (1)
Hoàn toàn tương tự ta có \(SA\perp KN\) (2)
(1); (2) \(\Rightarrow SA\perp\left(KMN\right)\)
d.
Từ A kẻ \(AH\perp SO\)
Do \(BD\perp\left(SAC\right)\) (cmt) \(\Rightarrow BD\perp AH\)
\(\Rightarrow AH\perp\left(SBD\right)\)
\(\Rightarrow AH=d\left(A;\left(SBD\right)\right)\)
\(SA=\sqrt{SB^2-AB^2}=2a\)
\(AC=a\sqrt{2}\Rightarrow AO=\dfrac{a\sqrt{2}}{2}\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AO^2}\Rightarrow AH=\dfrac{SA.OA}{\sqrt{SA^2+OA^2}}=\dfrac{2a}{3}\)
CM
6 tháng 7 2019
và do đó phương trình đã cho tương đương với
Vậy đáp án là D.
PT
1
CM
25 tháng 12 2019
Hàm số y 1 = sin π 2 − x có chu kì T 1 = 2 π − 1 = 2 π
Hàm số y 2 = cot x 3 có chu kì T 2 = π 1 3 = 3 π
Suy ra hàm số đã cho y = y 1 + y 2 có chu kì T = B C N N 2 , 3 π = 6 π .
Vậy đáp án là D.
PT
1
CM
9 tháng 4 2018
Mỗi lần cắt một mảnh giấy thành 7 mảnh, tức là Mạnh tạo thêm 6 mảnh giấy. Do đó công thức tính số mảnh giấy theo n bước được thực hiện là Sn = 6n + 1. Ta chứng minh tính đúng đắn của công thức trên bằng phương pháp quy nạp theo n.
Bước cơ sở. Mạnh cắt mảnh giấy thành 7 mảnh, n =1, S(1) = 6.1+1 =7
Công thức đúng với n = 1
Bước quy nạp: giả sử sau k bước, Mạnh nhận được số mảnh giấy là S(k) = 6k + 1
Sang bước thứ k +1, Mạnh lấy một trong số những mảnh giấy nhận được trong k bước trước và cắt thành 7 mảnh. Tức là Mạnh đã lấy đi 1 trong S(k) mảnh và thay vào đó 7 mảnh được cắt ra. Vậy tổng số mảnh giấy ở bước k + 1 là: S(k =1) = S(k) -1 + 7= S(k) + 6 = 6k + 1 + 1 = 6(k+1) +1
Vậy công thức S(n) đúng với mọi n ∈N* . Theo công thức trên chỉ có phương án D thoả mãn vì 121 =6.20 + 1
Đáp án D
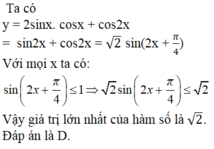
24.
\(y'=\dfrac{\left(sinx\right)'}{sinx}=\dfrac{cosx}{sinx}=cotx\)
25.
\(y'=\dfrac{\left(cosx+sinx\right)'}{cosx+sinx}=\dfrac{cosx-sinx}{cosx+sinx}\)
\(y'\left(\dfrac{\pi}{3}\right)=\dfrac{cos\left(\dfrac{\pi}{3}\right)-sin\left(\dfrac{\pi}{3}\right)}{cos\left(\dfrac{\pi}{3}\right)+sin\left(\dfrac{\pi}{3}\right)}=\sqrt{3}-2\)
26.
\(f'\left(x\right)=\dfrac{\left(2-\sqrt{2x+1}\right)'}{2-\sqrt{2x+1}}=\dfrac{-\dfrac{1}{\sqrt{2x+1}}}{2-\sqrt{2x+1}}\)
\(f'\left(0\right)=\dfrac{-\dfrac{1}{\sqrt{2.0+1}}}{2-\sqrt{2.0+1}}=-1\)
27.
\(y'=\dfrac{\left(x+\sqrt{1+x^2}\right)'}{x+\sqrt{1+x^2}}=\dfrac{1+\dfrac{x}{\sqrt{1+x^2}}}{x+\sqrt{1+x^2}}=\dfrac{1}{\sqrt{1+x^2}}\)
28.
\(y'=\dfrac{\left(\sqrt{1+e^x}-1\right)'}{\sqrt{1+e^x-1}}-\dfrac{\left(\sqrt{1+e^x}+1\right)'}{\sqrt{1+e^x}+1}\)
\(=\dfrac{\dfrac{e^x}{2\sqrt{1+e^x}}}{\sqrt{1+e^x}-1}-\dfrac{\dfrac{e^x}{2\sqrt{1+e^x}}}{\sqrt{1+e^x}+1}=\dfrac{e^x}{2\sqrt{1+e^x}}\left(\dfrac{1}{\sqrt{1+e^x}-1}-\dfrac{1}{\sqrt{1+e^x}+1}\right)\)
\(=\dfrac{e^x}{2\sqrt{1+e^x}}.\dfrac{2}{e^x}=\dfrac{1}{\sqrt{1+e^x}}\)