Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


5: \(\left(x+y\right)\left(x+2y\right)\left(x+3y\right)\left(x+4y\right)+y^4\)
\(=\left(x^2+5xy+4y^2\right)\left(x^2+5xy+6y^2\right)+y^4\)
\(=\left(x^2+5xy\right)^2+10y^2\left(x^2+5xy\right)+24y^4+y^4\)
\(=\left(x^2+5xy\right)^2+2\cdot\left(x^2+5xy\right)\cdot5y^2+\left(5y^2\right)^2\)
\(=\left(x^2+5xy+5y^2\right)^2\) là số chính phương
=>Mệnh đề này đúng
Mệnh đề phủ định là \(\overline{E}\) : \(\exists x,y\in R:\left(x+y\right)\left(x+2y\right)\left(x+3y\right)\left(x+4y\right)+y^4\) không là số chính phương
4: \(x\left(x+2\right)+y\left(y-4\right)+10\)
\(=x^2+2x+1+y^2-4y+4+5\)
\(=\left(x+1\right)^2+\left(y-2\right)^2+5\ge5>0\forall x,y\)
=>Mệnh đề này đúng
Mệnh đề phủ định là: \(\overline{D}:\) \(\exists x,y\in R:x\left(x+2\right)+y\left(y-4\right)+10\le0\)
3: \(2x^2+4xy+5y^2\)
\(=2x^2+4xy+2y^2+3y^2\)
\(=2\left(x+y\right)^2+3y^2\ge0\forall x,y\)
=>Mệnh đề này sai
Mệnh đề phủ định là: \(\overline{C}:\forall x,y\in R:2x^2+4xy+5y^2\ge0\)
1: TH1: n=3k
\(A=n^2+1=\left(3k\right)^2+1=9k^2+1\) không chia hết cho 3(1)
TH2: n=3k+1
\(A=n^2+1\)
\(=\left(3k+1\right)^2+1\)
\(=9k^2+6k+2=3\left(3k^2+2k\right)+2\) không chia hết cho 3(2)
TH3: n=3k+2
\(A=n^2+1\)
\(=\left(3k+2\right)^2+1\)
\(=9k^2+12k+4+1\)
\(=9k^2+12k+5=9k^2+12k+3+2=3\left(3k^2+4k+1\right)+2\) không chia hết cho 3(3)
Từ (1),(2),(3) suy ra A không chia hết cho 3
=>Mệnh đề này đúng
Mệnh đề phủ định là: \(\overline{A}:\exists n\in N:n^2+1\vdots3\)

Gọi O là trọng tâm tam giác ABC.
Dựng hình bình hành ABCE.
Ta có \(\overrightarrow{MA}+\overrightarrow{MB}+\overrightarrow{MC}=3\overrightarrow{MO}\).
\(\overrightarrow{MA}-\overrightarrow{MB}+\overrightarrow{MC}=\overrightarrow{BA}+\overrightarrow{MC}=\overrightarrow{CE}+\overrightarrow{MC}=\overrightarrow{ME}\).
Từ đó \(T=3MO+3ME\ge3OE\).
Dấu bằng xảy ra khi và chỉ khi M là giao của OE và AC, tức M là trung điểm của AC.
Vậy...


Mình giải được phần 1 rồi nhưng không biết cách viết bài giải để gửi cho bn :))), theo mình thì phần 1 bạn chuyển căn thứ nhất với căn thứ 3 thành 1 cặp, căn thứ hai với căn thứ tư thành một cặp sau đó nhân liên hợp nhé!



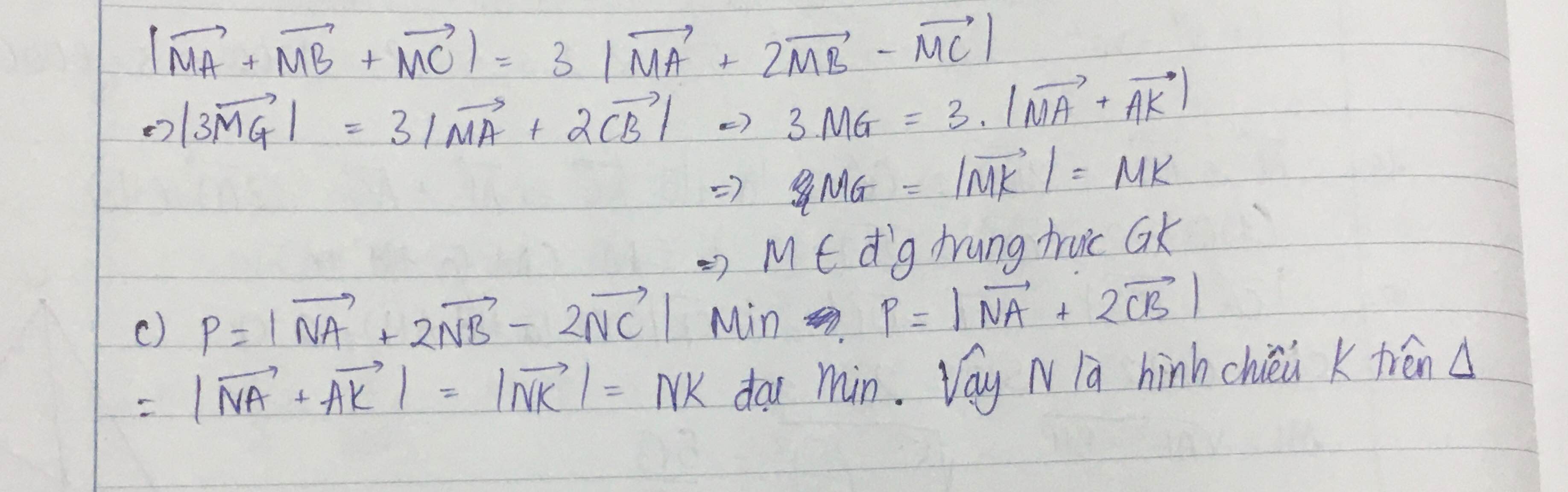 Từ câu a suy ra đc vecto AK = 2 lần vecto CB nhé.
Từ câu a suy ra đc vecto AK = 2 lần vecto CB nhé.

