Tìm các tam giác cân trên hình dưới.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 2 2018
+) Xét tam giác ABC có AB = AC nên tam giác ABC cân tại A.
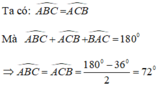
+) Xét tam giác ABD có góc ABC là góc ngoài tam giác tại đỉnh B nên:
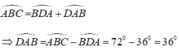
Do tam giác ABD có: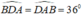 
nên tam giác ABD cân tại B.
+) Ta có:
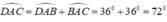
Tam giác ADC có: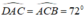 
nên tam giác ADC cân tại D.
+) Xét tam giác ACE có góc ACB là góc ngoài tam giác tại đỉnh C nên:
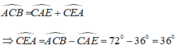
Do tam giác ACE có: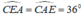 
nên tam giác ACE cân tại C.
+) Ta có:
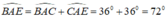
Tam giác ABE có: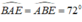 
nên tam giác ABE cân tại E.
+) Tam giác ADE có: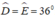 
nên tam giác này cân tại A.
Vậy có tất cả 6 tam giác đều là: ABD, ABC, ACE, AEB; ADC và ADE.
PT
Tính cạnh đáy BC của tam giác cân ABC trên các hình dưới đây. Trên hình bên trái: AH = 7cm; HC = 2cm
1
CM
6 tháng 2 2018
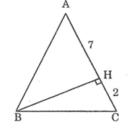
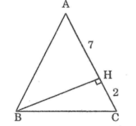
Tam giác ABC cân tại A ta có: AB = AC = CH + HA = 2 + 7 =9
Trong tam giác vuông BHA, ta có ∠(BHA) =90°
Áp dụng định lí pitago, ta có: AB2=BH2+HA2
Suy ra: BH2=AB2-AH2=92-72=81-49=32
Trong tam giác vuông BHC, ta có ∠(BHC) =90°
Áp dụng định lí pitago ta có: BC2=BH2+HC2 mà BH2 = 32, HC2 = 22 = 4
BC2 =32 + 4 =36 ⇒ BC = √36 = 6 cm
PT
Tính cạnh đáy BC của tam giác cân ABC trên các hình dưới đây. Trên hình bên phải: AH = 4cm; HC = 1cm
1
CM
17 tháng 7 2019
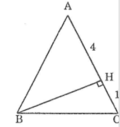
Tam giác ABC cân tại A nên ta có: AB=AC= AH + HC =4+1=5
Trong tam giác vuông BHA ta có ∠(BHA) =90°
Áp dụng định lí pitago, ta có: AB2=BH2+HA2
Suy ra: BH2=AB2-AH2=52-42=25-16=9
Trong tam giác vuông BHC, ta có ∠(BHC) =90°
Áp dụng định lí pitago ta có: BC2=BH2+HC2
BC2=9+1=10 =>BC=√10
CM
1 tháng 4 2018
Các tam giác cân trên hình 112:
-ΔADE cân tại A: có các cạnh bên là AD và AE; cạnh đáy: DE; góc D và góc E là hai góc ở đáy; góc A là góc ở đỉnh
-ΔABC cân tại A: có các cạnh bên là AB và AC; cạnh đáy: BC; góc B và góc C là hai góc ở đáy; góc A là góc ở đỉnh
-ΔAHC cân tại A: có các cạnh bên là AH và AC; cạnh đáy: HC; góc H và góc C là hai góc ở đáy; góc A là góc ở đỉnh
Tìm các tam giác cân trên hình vẽ sau
20 tháng 1 2022
Xét ΔBDC có:
\(\widehat{BDC}+\widehat{BCD}+\widehat{DBC}=180^o\\ \Rightarrow36^o+72^o+\widehat{BDC}=180^o\\ \Rightarrow\widehat{BDC}=72^o\)
Vì \(\widehat{BDC}=\widehat{BCD}\) nên ΔBDC cân tại B
Xét ΔABC có:
\(\widehat{ACB}+\widehat{ABC}+\widehat{BAC}=180^o\\ \Rightarrow36^o+72^o+\widehat{ABC}=180^o\\ \Rightarrow\widehat{ABC}=72^o\)
Vì \(\widehat{ABC}=\widehat{ACB}\) nên ΔABC cân tại A
LL
Giúp mình hình b với
1
PT
1
CM
13 tháng 1 2019
Đặt độ dài cạnh ô vuông là 1 (đơn vị chiều dài)
Áp dụng định lí pitago ta có:
AB2=12+22=1+4=5
BC2=12+22=1+4=5
AC2=32+12=9+1=10
Suy ra: AC2=AB2+BC2
Áp dụng định lí pitago đảo ta có tam giác ABC vuông tại B
Lại có: AB2=BC2=5 suy ra: AB = BC. Do đó, tam giác ABC là tam giác cân tại B.
Vậy tam giác ABC vuông cân tại B
LL
0
29 tháng 1 2021
a) Ta có: EF//BC(gt) =>\(\left\{{}\begin{matrix}\text{^EOB = ^OBC (SLT)}\\\text{ ^FOC = ^OCB (SLT)}\\\text{^AEF = ^B (Đồng vị)}\\\text{^AFE = ^C (Đồng vị)}\end{matrix}\right.\)
Có: ^OBC = ^OBA ( BF là phân giác ^B)
mà: ^EOB = ^OBC (cmt)
=> ^EOB = ^OBA => tam giác EBO cân tại E
Có: ^OCA = ^OCB ( BF là phân giác ^B)
mà: ^FOC = ^OCB (cmt)
=> ^FOC = ^OCA => tam giác FCO cân tại E
Ta có: ^AEF = ^B (cmt)
^AFE = ^C (cmt)
Mà ^B = ^C (tam giác ABC cân tại A)
=> ^AEF = ^AFE => tam giác AEF cân tại A
Có : ^ABF = ^CBF = \(\dfrac{1}{2}\) ^B ( BF là phân giác ^B)
^ACE = ^BCE = \(\dfrac{1}{2}\) ^B ( CF là phân giác ^C)
mà : ^B = ^C (tam giác ABC cân tại A)
=> ^ACE = ^ABF = ^CBF = ^BCE
Xét tg OBC có: ^OBC = ^OCB (^CBF = ^BCE) => tg OBC cân tại O
Xét tam giác FCO và tam giác EBO có:
^FOC = ^FOB ( đối đỉnh)
^FCO = ^EBO (^ABF = ^ACE)
OB = OC ( tg OBC cân tại O )
=> tam giác FCO = tam giác EBO(g-c-g)
Hình nào bạn