Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

câu a: có 2 bước
bước 1 : tính cạnh BH
ta có: AB = AC = 7 +2 =9
theo định lý Py -ta -go:
ta có : BH2 = AB2- HB2
BH2= 92-72
=>BH=\(\sqrt{32}\)
bước 2: tính cạnh BC
theo định lí Py-ta-go
ta có: BH2 + HC2=BC2
=>BC2= \(\sqrt{32}\)2 + 22 =36
=> BC = \(\sqrt{36}\) = 6
câu b: có 2 bước
bước 1: tìm cạnh BH
ta có AB = AC= 4+1=5
theo định lí Py-ta-go
ta có BH2 = AB2 - AH2
BH2 = 52-42
=> BH= 3
bước 2 : tìm cạnh BC
theo định lí Py-ta-go
ta có : BC2= HC2+BH2
BC2= 12+32
=>BC=\(\sqrt{10}\)
a)Xét tam giác ABC cân tại A\(\Rightarrow\)AB = AC 1
Mà AC = AH + HC =7 + 2 = 9 (cm) 2
Từ 1 và 2 \(\Rightarrow\)AB = AC = 9 (cm)
Xét tam giác ABH vuông tại H
Áp dụng định lí Py-ta-go,ta có:
AB2 = BH2 + AH2
\(\Rightarrow\)92 = BH2 + 72
BH2 = 92 - 72
BH2 = 81 - 49
BH2 = 32\(\Rightarrow\)BH = \(\sqrt[]{32}\) (cm)
Xét tam giác BHC vuông tại H
Áp dụng định lí Py-ta-go, ta có:
BC2 = BH2 + HC2
\(\Rightarrow\)BC2 = \(\sqrt[]{32}\)2 + 22
BC2 = 32 + 4
BC2 = 36\(\Rightarrow\)BC = 6 (cm)
b)Xét tam giác ABC cân tại A\(\Rightarrow\)AB = AC 1
Mà AC = AH + HC = 4 + 1 = 5 (cm) 2
Từ 1 và 2 \(\Rightarrow\)AB = AC = 5 (cm)
Xét tam giác ABH vuông tại H
Áp dụng định lí Py-ta-go, ta có:
AB2 = HB2 + AH2
\(\Rightarrow\)52 = HB2 + 42
HB2 = 52 - 42
HB2 = 25 - 16
HB2 = 9 \(\Rightarrow\)HB = 3 (cm)
Xét tam giác BHC vuông tại H
Áp dụng định lí Py-ta-go, ta có:
BC2 = HC2 + BH2
\(\Rightarrow\)BC2 = 12 + 32
BC2 = 1 + 9
BC2 = 10\(\Rightarrow\)BC = \(\sqrt[]{10}\) (cm)

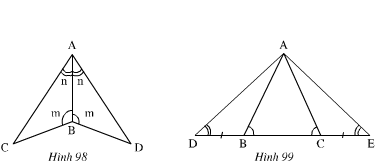
nh 98): Xét ΔABC và ΔABD có:
Nên ΔABC = ΔABD (g.c.g)
- Hình 99): Ta có:
Xét ΔABD và ΔACE có:
Nên ΔABD = ΔACE ( g.c.g)
Xét ΔADC và ΔAEB có:
DC = EB (Vì DC = DB + BC ; EB = EC + BC mà DB = EC)
Nên ΔADC = ΔAEB (g.c.g)
Xem hình 98)
∆ABC và ∆ABD có:
ˆA1A1^=ˆA2A2^(gt)
AB là cạnh chung.
ˆB1B1^=ˆB2B2^(gt)
Nên ∆ABC=∆ABD(g.c.g)
Xem hình 99)
Ta có:
ˆB1B1^+ˆB2B2^=1800 (Hai góc kề bù).
ˆC1C1^+ ˆC2C2^=1800 (Hai góc kề bù)
Mà ˆB2B2^=ˆC2C2^(gt)
Nên ˆB1B1^=ˆC1C1^
* ∆ABD và ∆ACE có:
ˆB1B1^=ˆC1C1^(cmt)
BD=EC(gt)
ˆDD^ = ˆEE^(gt)
Nên ∆ABD=∆ACE(g.c.g)
* ∆ADC và ∆AEB có:
ˆDD^=ˆEE^(gt)
ˆC2C2^=ˆB2B2^(gt)
DC=EB
Nên ∆ADC=∆AEB(g.c.g)

Tam giác DKE có:
+
+
=900 (tổng ba góc trong của tam giác).
+800 +400=1800
=1800 -1200=
Nên
∆ ABC và ∆KDE có:
AB=KD(gt)
=
=600và BE= ED(gt)
Do đó ∆ABC= ∆KDE(c.g.c)
Tam giác MNP không có góc xem giữa hai cạnh tam giác KDE ha ABC nên không bằng hai tam giác còn lại .
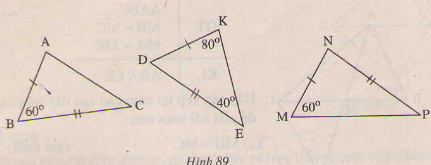
- Tam giác DKE có: ∠D + ∠K + ∠E = 1800 (tổng ba góc trong của tam giác).
hay ∠D + +800 +400 = 1800
⇒∠D = 1800 -1200 = 600
Xét ∆ ABC và ∆KDE có:
AB = KD(gt)
∠B = ∠D ( cùng = 600 )
và BE = ED (gt)
Do đó ∆ABC= ∆KDE (c.g.c)
- Tam giác MNP không có góc xem giữa hai cạnh tam giác KDE ha ABC nên không bằng hai tam giác còn lại .

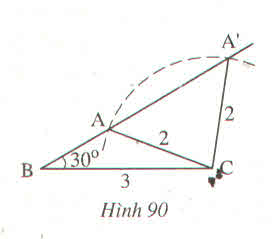
Góc ABC không phải là góc xen giữa BC và CA, Góc A'BC không phải là góc xen giữa hai cạnh BC và CA'. Do đó không thể sử dụng trường hợp cạnh góc cạnh để kết luận ∆ABC=∆A'B 'C' được.
Góc ABC không phải là góc xen giữa BC và CA, Góc A'BC không phải là góc xen giữa hai cạnh BC và CA'. Do đó không thể sử dụng trường hợp cạnh góc cạnh để kết luận ∆ABC=∆A'B 'C' được.

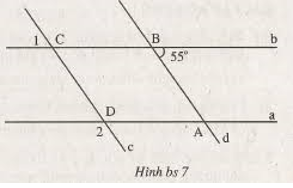
a) DE // AB, DE = \(\dfrac{1}{2}\)AB, IK // AB, IK = \(\dfrac{1}{2}\)AB
=> DE//IK và DE = IK
b) Xét tg GDE và tg GIK có:
DE = IK (cmt)
GDE = GIK (slt)
GED = GKI (slt)
=> tg GDE = tg GIK (g.c.g)
=> GD = GI ( c.t.ứ)
Có GD = GI = IA nên AG = \(\dfrac{2}{3}\)AD
Tính cạnh đáy BC của tam giác cân ABC trên các hình dưới đây. Trên hình bên trái: AH = 7cm; HC = 2cm
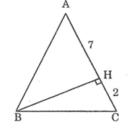
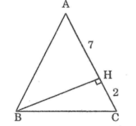

Tam giác ABC cân tại A ta có: AB = AC = CH + HA = 2 + 7 =9
Trong tam giác vuông BHA, ta có ∠(BHA) =90°
Áp dụng định lí pitago, ta có: AB2=BH2+HA2
Suy ra: BH2=AB2-AH2=92-72=81-49=32
Trong tam giác vuông BHC, ta có ∠(BHC) =90°
Áp dụng định lí pitago ta có: BC2=BH2+HC2 mà BH2 = 32, HC2 = 22 = 4
BC2 =32 + 4 =36 ⇒ BC = √36 = 6 cm
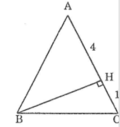
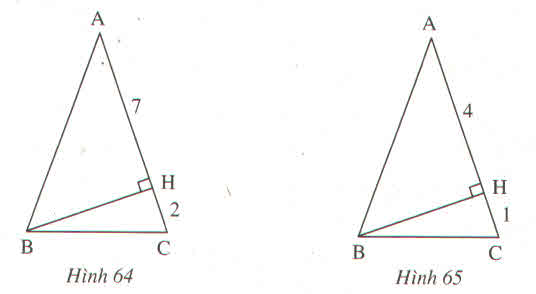










Tam giác ABC cân tại A nên ta có: AB=AC= AH + HC =4+1=5
Trong tam giác vuông BHA ta có ∠(BHA) =90°
Áp dụng định lí pitago, ta có: AB2=BH2+HA2
Suy ra: BH2=AB2-AH2=52-42=25-16=9
Trong tam giác vuông BHC, ta có ∠(BHC) =90°
Áp dụng định lí pitago ta có: BC2=BH2+HC2
BC2=9+1=10 =>BC=√10