Trong cách hình 116,117,118 tam giác nào là tam giác cân, tam giác nào là tam giác đều? Vì sao?Em cần hình 118 ạ!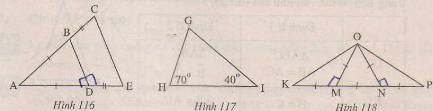
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
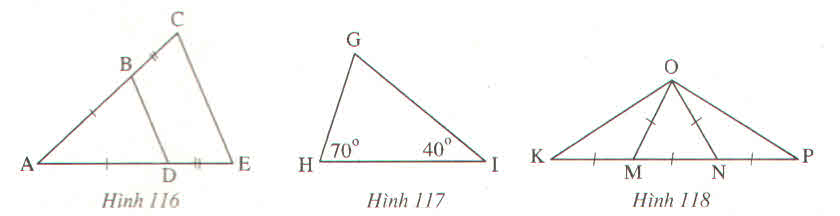
Hình 116.
Ta có: ∆ABD cân vì có AB=AD.
∆ACE cân vì AC=AE(do AB=AD,BC=DE nên AB+BC+AD+DE nên AB + BC= AD+DE hay AC= AE).
Hình 117.
Ta tính được
G= 1800-(H+I) = 1800 - (700+400)= 700
Nên ∆GHI cân vì(G=H)
Hình 118.
∆OMK là tam giác cân vì OM= MK
∆ONP là tam giác cân vì ON=OP
∆OKP là tam giác cân là vì K = P
Suy ra OKM+KOM=600
mà OKM = KOM nên =300
Tương tự OPM =300

- Hình 116
Ta có ΔABD cân vì AB = AD
ΔACE cân vì AC = AE
Do AB = AD , BC = DE nên AB + BC = AD + DE hay AC = AE
⇒ ΔACE cân
- Hình 117
Ta tính được
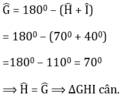
- Hình 118
* ΔOMN là tam giác đều vì ba cạnh bằng nhau OM = MN = NO
* ΔOMK cân tại M vì OM = MK
* ΔONP là tam giác cân tại N vì ON = NP


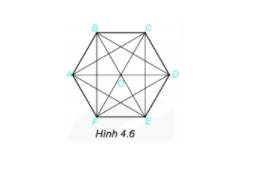
Các tam giác đều ghép thành hình lục giác đều là: tam giác ABO, tam giác BCO, tam giác CDO, tam giác DEO, tam giác EFO, tam giác FAO.
Trong hình còn có các tam giác đều: ACE, BDF.

* tam giác đều
- chứng minh tam giác có 3 cạnh = nhau
- chứng minh tam giác có 3 góc = nhau
- chứng minh tam giác có 2 góc = 60*
- chứng minh tam giác cân có 1 góc = 60*
Có tổng cộng 4 cách nha
ngoài 4 cách ấy ra,đang còn một cách nx đó là:2 đường cao vừa là phân giác vừa là trung tuyến
học tốt!

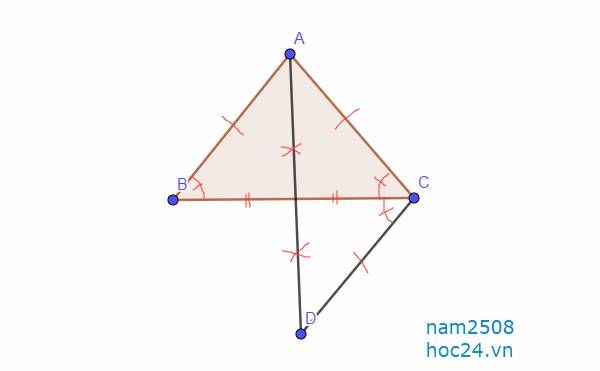
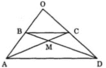
a, Diện tích BAD = diện tích CAD (chung đáy AD, các đường cao vẽ từ B, C đến AD bằng nhau)
Diện tích ABC = diện tích BDC (chung đáy BC, các đường cao vẽ từ A và D đến BC bằng nhau)
Suy ra diện tích ABM bằng diện tích DCM
b, Diện tích ABC = diện tích DBC = diện tích OBC (chung đáy BC và 3 đường cao vẽ từ A, D, O đến BC bằng nhau)

\(\text{#TNam}\)
`a,` Vì Tam giác `ABC` cân tại `A -> AB=AC,` \(\widehat{B}=\widehat{C}\)
Xét Tam giác `ABM` và Tam giác `ACM:`
`AB=AC (CMT)`
\(\widehat{B}=\widehat{C}\)
`MB=MC (g``t)`
`=> \text {Tam giác ABM = Tam giác ACM (c-g-c)}`
`b,` Xét Tam giác `AMB` và Tam giác `CMD:`
`AM=MD (g``t)`
\(\widehat{AMB}=\widehat{CMD}\) `( \text {2 góc đối đỉnh})`
`MB = MC (g``t)`
`=> \text {Tam giác AMB = Tam giác CMD (c-g-c)}`
`->`\(\widehat{ABC}=\widehat{DCB}\) `(\text {2 góc tương ứng})`
Mà `2` góc này nằm ở vị trí sole trong
`-> \text {AB // CD}`
`c,` Vì Tam giác `AMB =` Tam giác `CMD (b)`
`-> AB=CD (\text {2 cạnh tương ứng})`
Mà `AB = AC (a)`
`-> AC = CD`
Xét Tam giác `ACD: AC = CD`
`-> \text {Tam giác ACD cân tại C}`

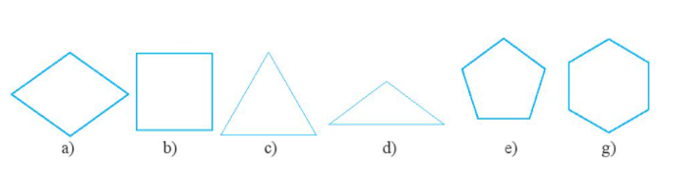
Hình vuông là b), tam giác đều là c), lục giác đều là g).
Hình vuông là a), tam giác đều là d), lục giác đều là e).
Hình vuông là b), tam giác đều là d), lục giác đều là e).
Hình vuông là a), tam giác đều là c), lục giác đều là g).
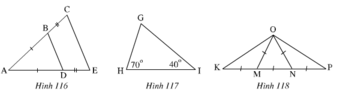

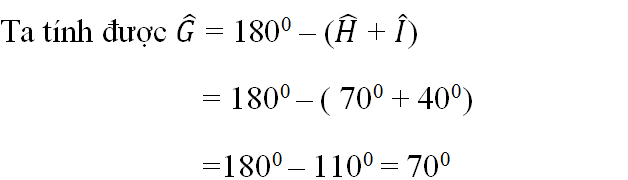

Hình 118 :
Có : OM = ON = MN nên tam giác OMN đều
=> góc OMN = góc ONM
Mà : góc OMK + góc OMN = 180 độ
góc ONP + góc ONM = 180 độ
=> góc OMK = góc ONP
=> tam giác OMK = tam giác ONP ( c.g.c )
=> OK = OP ( 2 cạnh tương ứng )
=> tam giác OKP cân tại 0
Tk mk nha
Hình 118 :
Vì tam giác MKO = tam giac NPO ( c-g-c)
=> KO = OP => tam giac KOP cân tại O
còn mấy tam giac kia thì dễ rồi