Bài 3 : Tìm nghiệm
c) C(x) = x4 +2x2 +8
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 3 2022
a. cậu thu gọn bằng cách dùng t/c kết hợp và giao hoán
b. cậu thay từng giá vào biểu thức vừa được rút gọn để tìm
c. thì.... tớ ko biết
CM
1 tháng 9 2018
c. Thay x = -1 vào A(x) và B(x) ta có:
A(-1) = 0, B(-1) = 2
Vậy x = -1 là nghiệm của A(x) nhưng không là nghiệm của B(x) (1 điểm)
NP
23 tháng 12 2022
a/ 2x^2 (x – 1) + 4x (1 – x)
= 2x^2(x – 1) – 4x (x – 1)
= (x – 1)( 2x^2 – 4x)
=2x(x – 1)(x – 2)
TN
1
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2022
\(x^4+2x^2-3=0\Leftrightarrow x^4+3x^2-x^2-3=0\)
\(\Leftrightarrow x^2\left(x+3\right)-\left(x^2+3\right)=0\)
\(\Leftrightarrow\left(x^2+3\right)\left(x^2-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2=-3\left(vn\right)\\x^2=1\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
\(\Rightarrow-1+1=0\)
CM
11 tháng 3 2019
Từ đồ thị hàm số, suy ra phương trình x 4 - 2 x 2 - 3 = 2 m - 4 có hai nghiệm phân biệt khi và chỉ khi
TC
6 tháng 5 2022
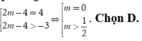
a) cho A(x) = 0
\(=>2x^2-4x=0\)
\(x\left(2-4x\right)=0\Rightarrow\left[{}\begin{matrix}x=0\\4x=2\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\end{matrix}\right.\)
b)\(B\left(y\right)=4y-8\)
cho B(y) = 0
\(4y-8=0\Rightarrow4y=8\Rightarrow y=2\)
c)\(C\left(t\right)=3t^2-6\)
cho C(t) = 0
\(=>3t^2-6=0=>3t^2=6=>t^2=2\left[{}\begin{matrix}t=\sqrt{2}\\t=-\sqrt{2}\end{matrix}\right.\)
TC
6 tháng 5 2022
d)\(M\left(x\right)=2x^2+1\)
cho M(x) = 0
\(2x^2+1=0\Rightarrow2x^2=-1\Rightarrow x^2=-\dfrac{1}{2}\left(vl\right)\)
vậy M(x) vô nghiệm
e) cho N(x) = 0
\(2x^2-8=0\)
\(2\left(x^2-4\right)=0\)
\(2\left(x^2+2x-2x-4\right)=0\)
\(2\left(x-2\right)\left(x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x-2=0\\x+2=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=2\\x=-2\end{matrix}\right.\)
13 tháng 12 2022
ĐKXĐ: x<>2
x^4-2x^2-8/x-2=0
=>x^4-2x^2-8=0
=>(x^2-4)(x^2+2)=0
=>x^2-4=0
=>x=-2
CM
8 tháng 10 2019
Đáp án A
Xét hàm y = x 4 – 2 x 2 – 3
Ta có: y’ = 4x3 – 4x
⇒ y’ = 0 ⇔ x = 0 hoặc x = -1 hoặc x = 1
Ta có bảng biến thiên
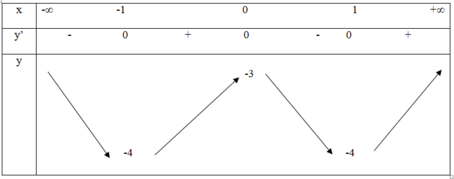
Số phương trình có 2 nghiệm phân biệt
bằng số giao điểm giữa đồ thị hàm số y = x 4 – 2 x 2 – 3 và đường thẳng y = m
ð ⇒ m = -4 hoặc m > -3
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 4 2021
\(A\left(x\right)+B\left(x\right)-C\left(x\right)\)
\(=\left(-7+2x^2+x^4+3x^5-x^3\right)+\left(-x+x^4+2x^3-7\right)-\left(2x-x^4-3x^3\right)\)
\(=3x^5+3x^4+4x^3+2x^2-3x-14\)
C(x) có nghiệm khi
x4 + 2x2 + 8 = 0
mà x4 + 2x2 + 8 = x2(x2 + 2) + 8 \(\ge8>0\)
=> C(x) vô nghiệm
\(C\left(x\right)=x^4+2x^2+8\)
\(\text{Ta có:}\)\(x^4\ge0\)
\(2x^2\ge0\)
\(\rightarrow x^4+2x^2\ge0\)
\(\rightarrow x^4+2x^2+8\ge8\)
\(\rightarrow C\left(x\right)\ge8\)
\(\rightarrow C\left(x\right)>0\ne0\)
\(\rightarrow C\left(x\right)\text{không có nghiệm nào thỏa mãn}\)
\(\text{Vậy đa thức vô nghiệm}\)