Cho \(\Delta ABC=\Delta D\text{EF}\) .Biết \(\widehat{B}\)=\(60^o\),AB=3cm,EF=4cm.Tính \(\widehat{E}\),BC,DE?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


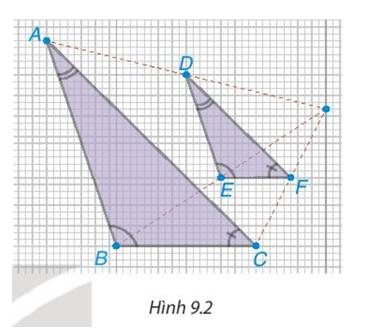
Ta có: \(\frac{{AB}}{{DE}} = 2{;^{}}\frac{{BC}}{{EF}} = 2{;^{}}\frac{{AC}}{{DF}} = 2\)
Ta có:\(\dfrac{AB}{DE}=2;\dfrac{BC}{EF}=2;\dfrac{AC}{DF}=2\)

Bạn xem lại xem có viết nhầm đề không. Theo hình vẽ thì 2 góc không bằng nhau.

Mình nghĩ bạn viết nhầm đề. Lời giải bài tương tự ở đây:
https://hoc24.vn/cau-hoi/cho-tam-giac-abc-vuong-tai-a-tren-cac-canh-abbcca-lan-luot-lay-cac-diem-def-sao-cho-deperp-bc-dedf-goi-m-la-trung-diem-cua-ef-chung-minh.260248714837

1/ Ta có: tam giác ABC = tam giác DEF
=> góc A = góc D
góc B = góc E
góc C = góc F
Ta có: góc A + góc B + góc C = 1800
1300 + góc C = 1800
góc C = 1800-1300 = 500
Ta có: góc A + góc B = 1300
góc A + 550 = 1300
góc A = 1300 - 550 =750
Vậy góc A = góc D = 750
góc B = góc E = 550
góc C = góc F = 500
2/ Ta có: tam giác DEF = tam giác MNP
=> DE = MN
EF = NP
FD = PM
Ta có: EF + FD = 10 cm
Mà NP - MP = EF - FD = 2 cm
EF = (10 + 2) : 2 = 6 (cm)
FD = (10 - 2) : 2 = 4 (cm)
Vậy DE = MN = 3 cm
EF = NP = 6 cm
FD = MP = 4 cm
1) Ta có: ( \(\widehat{A}\) + \(\widehat{B}\)) + \(\widehat{C}\) = 180o
hay 130o + \(\widehat{C}\) = 180o
\(\Rightarrow\) \(\widehat{C}\) = 180o - 130o = 50o
Vì ΔABC = ΔDEF nên ta có:
\(\widehat{C}\) = \(\widehat{F}\) = 50o
\(\widehat{E}\) = \(\widehat{B}\) = 55o
Ta có: \(\widehat{A}\) + \(\widehat{B}\) = 130o hay \(\widehat{A}\) + 55o = 130o
\(\Rightarrow\) \(\widehat{A}\) = 130o - 55o = 75o
\(\Leftrightarrow\) \(\widehat{A}\) = \(\widehat{D}\) = 75o
Vậy: \(\widehat{A}\) = \(\widehat{D}\) = 75o
\(\widehat{B}\) = \(\widehat{E}\) = 55o
\(\widehat{C}\) = \(\widehat{F}\) = 50o
2) ΔDEF = ΔMNP nên:
\(\Rightarrow\) DE = MN
EF = NP
FD = PM
Ta có: EF + FD = 10cm
mà ΔDEF = ΔMNP
\(\Rightarrow\) NP - MP = EF - FD = 2cm
\(\Rightarrow\) EF = \(\frac{10+2}{2}\) = 6cm
FD = 6cm - 2cm = 4cm
Vậy: DE= MN = 3cm
EF = NP = 6cm
FD = PM = 4cm

Vì \(\Delta{DEF}=\Delta{HIK}\)
\( \Rightarrow \widehat D = \widehat H\)( 2 góc tương ứng )
Mà \(\widehat D =73^0\)
\( \Rightarrow \widehat H=73^0\)
Vì \(\Delta{DEF}=\Delta{HIK}\)
\(\Rightarrow DE = HI;EF = IK;DF = HK\)( các cạnh tương ứng )
Vậy \( \widehat H = {73^o}; HI = 5cm; EF = 7cm\)

Vì ΔABC ∽ ΔDEF \( \Rightarrow \widehat A = \widehat D{,^{}}\widehat B = \widehat E{,^{}}\widehat C = \widehat F\)
Mà \(\widehat A = {60^o} \Rightarrow \widehat D = {60^o}\)
\(\widehat E = {80^o} \Rightarrow \widehat B = {80^o}\)
Có \(\widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat C = \widehat F = {180^o} - {60^o} - {80^o} = {40^o}\)

Xét tam giác vuông ABC và tam giác vuông ADE có :
AB=AD
AC=AE
=> tam giác ABC= tam giác ADE ( 2 cạnh góc vuông )

Bài 4:
a: Xét ΔABE và ΔACD có
AB=AC
\(\widehat{ABE}=\widehat{ACD}\)
BE=CD
Do đó: ΔABE=ΔACD
Suy ra: \(\widehat{EAB}=\widehat{DAC}\)
b: ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
Ta có: ΔADE cân tại A
mà AM là đường cao
nên AM là phân giác của góc DAE
c: Xét ΔDAE cân tại A có \(\widehat{DAE}=60^0\)
nên ΔDAE đều
Nhận xét: Các góc trong ΔAED bằng nhau và cùng bằng 60 độ
góc E=góc B=60o (2 góc tương ứng)
BC=EF=4cm(2 cạnh tương ứng)
DE=AB=3cm(2 cạnh tương ứng)
Vậy...............
Vì t/g ABC = DEF ( c.g.c ) nên :
Góc E = Góc B = 60 độ ( 2 góc tương ứng )
BC = EF = 4 cm ( 2 cạnh tương ứng )
DE = AB = 3 cm ( 2 cạnh tương ứng )