Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

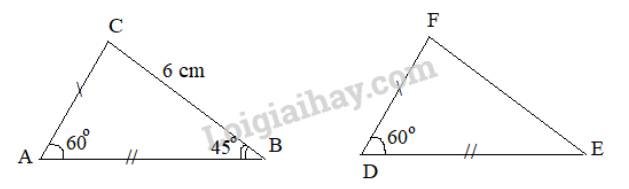
Xét hai tam giác ABC và DEF có:
\(\begin{array}{l}AB = DE\\AC = DF\\\widehat {BAC} = \widehat {EDF} (= {60^\circ })\end{array}\)
\(\Rightarrow \Delta ABC = \Delta DEF\)(c.g.c)
Do đó:
\(BC=EF = 6cm\) ( 2 cạnh tương ứng)
\( \widehat {ABC} =\widehat {DEF}= {45^o}\) (2 góc tương ứng)
\(\begin{array}{l}\widehat {BAC} + \widehat {ABC} + \widehat {ACB} = {180^o}\\ \Rightarrow {60^o} + {45^o} + \widehat {ACB} = {180^o}\\ \Rightarrow \widehat {ACB} = {75^o}\end{array}\)
\( \Rightarrow \widehat {EFD} = \widehat {ACB} = {75^o}\)

- Ta có: \(\widehat{ABE}+\widehat{CAE}=90^0\) (AB⊥AC tại A).
\(\widehat{AEH}+\widehat{HAE}=90^0\) (△AHE vuông tại H).
Mà \(\widehat{CAE}=\widehat{HAE}\) (AE là phân giác của \(\widehat{HAC}\)).
=>\(\widehat{ABE}=\widehat{AEH}\).
=>△ABE cân tại B.
=>\(AB=BE\).
- Ta có: \(\widehat{DAC}+\widehat{BAD}=90^0\) (AB⊥AC tại A).
\(\widehat{HAD}+\widehat{ADH}=90^0\) (△AHE vuông tại H).
Mà \(\widehat{BAD}=\widehat{HAD}\) (AD là phân giác của \(\widehat{HAB}\)).
=>\(\widehat{DAC}=\widehat{ADH}\).
=>△ACD cân tại C.
=>\(AC=CD\).
- Xét △ABC vuông tại A có:
\(BC^2=AB^2+AC^2\) (định lí Py-ta-go).
=>\(BC^2=5^2+12^2\).
=>\(BC^2=169\).
=>\(BC=13\) (cm).
\(AB+AC-BC=BE+CD-BC=BE+CD-BE-CE=CD-CE=DE\)=>\(DE=5+12-13=4\) (cm).

a) Xét ∆DEI và ∆DFI có:
DI là cạnh chung
DE = DF ( ∆DEF cân)
IE = IF (I là trung điểm của EF )
\(\Rightarrow\) ∆DEI = ∆DFI (c.c.c)
b) Vì ∆DEI = ∆DFI \(\Rightarrow\widehat{DIE}=\widehat{DIF}\)
mà \(\widehat{DIE}+\widehat{DIF}=180^o\) ( kề bù)
\(\Rightarrow\widehat{DIE}=\widehat{DIF}=180^o:2=90^o\)
c) I là trung điểm của EF nên IE = IF = 5cm
Xét ∆DEI vuông tại I
\(\Rightarrow\)DI2 = DE2 – EI2 (định lí pytago)
\(\Rightarrow\) DI2 = \(\sqrt{13^2-5^2}\) \(\sqrt{144}\)
\(\Rightarrow\) DI = 12 cm

Ta có: tam giác DEF = tam giác HIK
=> DE = HI ; EF = IK ; DF = HK
=> góc D = góc H
góc E = góc I
góc F = góc K
a/ Ta có: góc E = góc I (vì tam giác DEF = HIK)
Mà góc E = 400 => góc I = 400
b/ Chu vi tam giác DEF= chu vi tam giác HIK
= DE + EF + HK = DE+EF+DF=2+5+6=13 (cm)
Vậy chu vi tam giác DEF = chu vi tam giác HIK = 13 cm

1/ Ta có: tam giác ABC = tam giác DEF
=> góc A = góc D
góc B = góc E
góc C = góc F
Ta có: góc A + góc B + góc C = 1800
1300 + góc C = 1800
góc C = 1800-1300 = 500
Ta có: góc A + góc B = 1300
góc A + 550 = 1300
góc A = 1300 - 550 =750
Vậy góc A = góc D = 750
góc B = góc E = 550
góc C = góc F = 500
2/ Ta có: tam giác DEF = tam giác MNP
=> DE = MN
EF = NP
FD = PM
Ta có: EF + FD = 10 cm
Mà NP - MP = EF - FD = 2 cm
EF = (10 + 2) : 2 = 6 (cm)
FD = (10 - 2) : 2 = 4 (cm)
Vậy DE = MN = 3 cm
EF = NP = 6 cm
FD = MP = 4 cm
1) Ta có: ( \(\widehat{A}\) + \(\widehat{B}\)) + \(\widehat{C}\) = 180o
hay 130o + \(\widehat{C}\) = 180o
\(\Rightarrow\) \(\widehat{C}\) = 180o - 130o = 50o
Vì ΔABC = ΔDEF nên ta có:
\(\widehat{C}\) = \(\widehat{F}\) = 50o
\(\widehat{E}\) = \(\widehat{B}\) = 55o
Ta có: \(\widehat{A}\) + \(\widehat{B}\) = 130o hay \(\widehat{A}\) + 55o = 130o
\(\Rightarrow\) \(\widehat{A}\) = 130o - 55o = 75o
\(\Leftrightarrow\) \(\widehat{A}\) = \(\widehat{D}\) = 75o
Vậy: \(\widehat{A}\) = \(\widehat{D}\) = 75o
\(\widehat{B}\) = \(\widehat{E}\) = 55o
\(\widehat{C}\) = \(\widehat{F}\) = 50o
2) ΔDEF = ΔMNP nên:
\(\Rightarrow\) DE = MN
EF = NP
FD = PM
Ta có: EF + FD = 10cm
mà ΔDEF = ΔMNP
\(\Rightarrow\) NP - MP = EF - FD = 2cm
\(\Rightarrow\) EF = \(\frac{10+2}{2}\) = 6cm
FD = 6cm - 2cm = 4cm
Vậy: DE= MN = 3cm
EF = NP = 6cm
FD = PM = 4cm
Vì \(\Delta{DEF}=\Delta{HIK}\)
\( \Rightarrow \widehat D = \widehat H\)( 2 góc tương ứng )
Mà \(\widehat D =73^0\)
\( \Rightarrow \widehat H=73^0\)
Vì \(\Delta{DEF}=\Delta{HIK}\)
\(\Rightarrow DE = HI;EF = IK;DF = HK\)( các cạnh tương ứng )
Vậy \( \widehat H = {73^o}; HI = 5cm; EF = 7cm\)