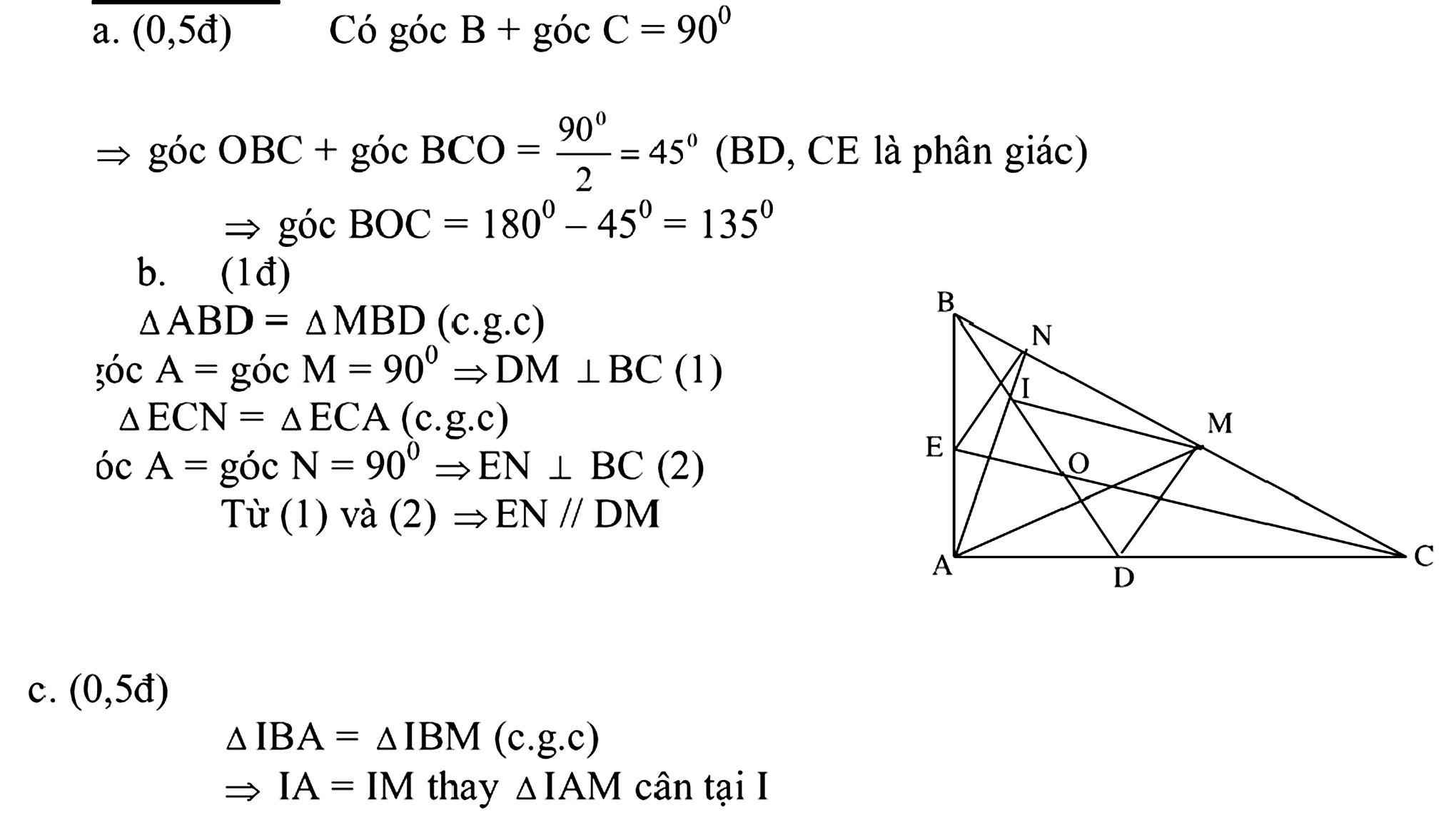
BT3: Cho tam giác ABC có góc A= 90 độ. Vẽ phân giác BD và CE ( D thuộc ac, e thuộc AB) chúng cắt nhau tại O
a) tính số đo goác BOC
b) Trên BC lấy M, N sao cho BM= BA, CN=CA. Chứng minh: EN// DM
c) Gọi I là giao điểm của BD và AN. Chứng minh: tam giác AIM vuông cân

Câu hỏi của Công chúa thủy tề - Toán lớp 7 - Học toán với OnlineMath
Em tham khảo tại link trên nhé.
Chứng minh bất đẳng thức
\(\frac{x}{2x+y+z}+\frac{y}{2y+z+x}+\frac{z}{2z+x+y}\le\frac{3}{4}\)
Con này mất dạy v:, chuyện đó tính sau
肖战 - Trang của 肖战 - Học toán với OnlineMath
Nó copy dữ dội trên này lắm
Câu hỏi của 凯原 - Ngữ Văn lớp 7 - Học toán với OnlineMath
Câu hỏi của Phương' ss ngốc - Ngữ Văn lớp 7 - Học toán với OnlineMath
Câu hỏi của Khanh Linh Ha - Toán lớp 7 - Học toán với OnlineMath
Câu hỏi của kudoshinichi - Tiếng Việt lớp 5 - Học toán với OnlineMath
Còn nhiù nhưng ko có t/g để cop