Cho hàm số y=2x2 có đồ thị (P). Xác định để đường thẳng y=2x+m cắt P tại 2 điểm phân biệt nằm trong góc phần tư thứ 1
Giải giúp vs lát óc rồi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 5 2021
Xét pt hoành độ giao điểm:
(m - 3)x + 2m - 4 = -x + 5
\(\Leftrightarrow\) mx - 3x + 2m - 4 = -x + 5
\(\Leftrightarrow\) m(x + 2) = 2x + 9
\(\Leftrightarrow\) m = \(\dfrac{2x+9}{x+2}\)
Vì 2 đường thẳng cắt nhau tại 1 điểm nằm trong góc phần tư thứ 1
\(\Rightarrow\) x > 0
\(\Leftrightarrow\) 2x + 9 > 9; x + 2 > 2
\(\Rightarrow\) \(\dfrac{2x+9}{x+2}>\dfrac{9}{2}\)
\(\Leftrightarrow\) m \(>\dfrac{9}{2}\)
Vậy \(m>\dfrac{9}{2}\)
Chúc bn học tốt!
TH
2
CM
15 tháng 1 2018
Đáp án là C.
• Xét hàm số y = x 4 − 2 x 2 + 2
+ y ' = 4 x 3 − 4 x , cho y ' = 0 ⇔ x = 0 ⇒ y = 2 x = ± 1 ⇒ y = 1
+ BBT
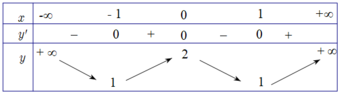
• Để đường thẳng y = m cắt đồ thị hàm số tại 4 điểm phân biệt thì 1 < m < 2.
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 12 2020
Phương trình hoành độ giao điểm:
\(x^2+3x=x+m^2\Leftrightarrow x^2+2x-m^2=0\)
Pt đã cho luôn có 2 nghiệm pb
\(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1x_2=-m^2\end{matrix}\right.\)
Do I là trung điểm đoạn AB \(\Leftrightarrow\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=-1\\y_I=\dfrac{y_A+y_B}{2}=\dfrac{x_A+m^2+x_B+m^2}{2}=m^2-1\end{matrix}\right.\)
Mà I thuộc d'
\(\Leftrightarrow y_I=2x_I+3\Leftrightarrow m^2-1=2.\left(-1\right)+3\)
\(\Leftrightarrow m^2=2\Rightarrow m=\pm\sqrt{2}\)
\(\Rightarrow\sum m^2=4\)
CM
27 tháng 7 2017
Chọn B.
Phương trình hoành độ giao điểm:
x
+
2
2
x
+
1
= mx + m - 1 
Để đường thẳng luôn cắt đồ thị hàm số tại hai điểm phân biệt thuộc hai nhánh của đồ thị thì phương trình (1) phải có hai nghiệm phân biệt
x
1
,
x
2
thỏa mãn 
(1) có hai nghiệm phân biệt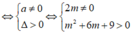 
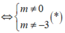
Theo định lý Vi – ét ta có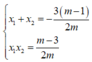 
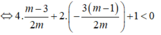
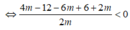
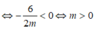
MT
29 tháng 4 2017
Các bạn giải nhanh giùm nha.mk gấp lắm. Cảm mơn mí bạn trc nha
Xét pt hoành độ gđ của (P) và (d) có:
\(2x^2=2x+m\)
\(\Leftrightarrow2x^2-2x-m=0\) (1)
Để (d) cắt (P) tại hai điểm nằm trong góc phần tư thứ 1
<=> pt (1) có hai nghiệm pb dương (không cần xét tung độ bởi tung độ luôn dương)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\x_1+x_2>0\\x_1x_2>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}4-4.2.\left(-m\right)>0\\1>0\left(lđ\right)\\-\dfrac{m}{2}>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m>-\dfrac{1}{2}\\m< 0\end{matrix}\right.\)
\(\Rightarrow\)\(-\dfrac{1}{2}< m< 0\)