x2-3y22+2xy+4y-1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 10 2017
x2 + 4x – 2xy – 4y + y2 = (x2-2xy+ y2) + (4x – 4y) → bạn Việt dùng phương pháp nhóm hạng tử
= (x - y)2 + 4(x – y) → bạn Việt dùng phương pháp dùng hằng đẳng thức và đặt nhân tử chung
= (x – y)(x – y + 4) → bạn Việt dùng phương pháp đặt nhân tử chung
AH
Akai Haruma
Giáo viên
28 tháng 8 2021
Lời giải:
a. $x^2+y^2+4y+13-6x$
$=(x^2-6x+9)+(y^2+4y+4)$
$=(x-3)^2+(y+2)^2$
b.
$4x^2-4xy+1+2y^2-2y$
$=(4x^2-4xy+y^2)+(y^2-2y+1)$
$=(2x-y)^2+(y-1)^2$
c.
$x^2-2xy+2y^2+2y+1$
$=(x^2-2xy+y^2)+(y^2+2y+1)$
$=(x-y)^2+(y+1)^2$
NT
28 tháng 8 2021
a. \(x^2+y^2+4y+12-6x=\left(x^2-6x+9\right)+\left(y^2+4y+4\right)=\left(x-3\right)^2+\left(y+2\right)^2\)b. \(4x^2-4xy+1+2y^2-2y=\left(4x^2-4xy+y^2\right)+\left(y^2-2y+1\right)=\left(2x-y\right)^2+\left(y-1\right)^2\)c. \(x^2-2xy+2y^2+2y+1=\left(x^2-2xy+y^2\right)+\left(y^2+2y+1\right)=\left(x-y\right)^2+\left(y+1\right)^2\)
PT
1
CM
29 tháng 4 2019
A = x 2 + 2 x y + y 2 – 4 x – 4 y + 1 = ( x 2 + 2 x y + y 2 ) – ( 4 x + 4 y ) + 1 = ( x + y ) 2 – 4 ( x + y ) + 1
Tại x + y = 3, ta có: A = 3 2 – 4.3 + 1 = -2
Đáp án cần chọn là: D
17 tháng 7 2021
Ta có: \(A=\left(x^2+2xy+y^2\right)-4x-4y+1\)
\(=\left(x+y\right)^2-4\left(x+y\right)+1\)
\(=3^2-4\cdot3+1\)
\(=-2\)
H9
HT.Phong (9A5)
CTVHS
10 tháng 8 2023
\(x^2-2xy+5y^2+4y+1\)
\(=x^2-2xy+y^2+4y^2+4y+1\)
\(=\left(x^2-2xy+y^2\right)+\left(4y^2+4y+1\right)\)
\(=\left(x-y\right)^2+\left(2y+1\right)^2\)
10 tháng 8 2023
\(x^2-2xy+5y^2+4y+1=x^2-2xy+y^2+4y^2+4y+1=\left(x-y\right)^2+\left(2y+1\right)^2\)
TL
1
23 tháng 10 2021
\(a,=3\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{1}{4}=3\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\ge\dfrac{1}{4}\)
Dấu \("="\Leftrightarrow x=\dfrac{1}{2}\)
\(b,=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
\(c,=\left(x^2-2xy+y^2\right)+x^2+1=\left(x-y\right)^2+x^2+1\ge1\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=y\\x=0\end{matrix}\right.\Leftrightarrow x=y=0\)
KH
0
PT
2
23 tháng 1 2022
x^2+4x-2xy-4y+y^2=(x^2-2xy+y^2)+(4x-4y)
=(x-y)^2+4(x-y)
=(x-y)(x-y+4)
PT
1
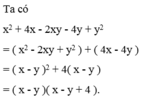
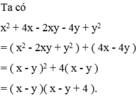
Đề bài là j z