K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 4 2018
tớ chỉ làm được phần a)thôi
ta có:\(\left(x-\frac{2}{3}\right):\frac{-3}{7}=\frac{-9}{11}\)
\(x-\frac{2}{3}=\frac{-9}{11}.\frac{-3}{7}\)
\(x-\frac{2}{3}=\frac{27}{77}\)
\(x=\frac{27}{77}+\frac{2}{3}\)
\(x=\frac{235}{231}\)
vậy x=\(\frac{235}{231}\)
LL
16 tháng 4 2018
a) \(\left(x-\frac{2}{3}\right)\):\(\frac{-3}{7}\)=\(\frac{-9}{1}\)
\(x-\frac{2}{3}\)=\(-9\cdot\frac{-3}{7}\)
\(x-\frac{2}{3}\)= \(\frac{27}{7}\)
\(x\)= \(\frac{27}{7}\)\(+\frac{2}{3}\)
\(x\)=\(\frac{95}{21}\)
b)\(x:2+x:\frac{5}{2}+x:\frac{1}{3}=\frac{-18}{25}\)
\(x:\left(2+\frac{5}{2}+\frac{1}{3}\right)=\frac{-18}{25}\)
\(x:\frac{12+15+2}{6}=\frac{-18}{25}\)
\(x:\frac{29}{6}=\frac{-18}{25}\)
\(x=\frac{-18}{25}\cdot\frac{29}{6}\)
\(x=\frac{-87}{25}\)
10 tháng 9 2023
\(a.n_{Zn}=\dfrac{13}{65}=0,2mol\\ Zn+2HCl\rightarrow ZnCl_2+H_2\uparrow\)
0,2 0,4 0,2 0,2
\(V_{H_2}=0,2.24,79=4,958l\\ b.m_{ZnCl_2}=0,2.136=27,2g\\ c.m_{dd\left(sau.pư\right)}=\dfrac{0,4.36,5}{7,3}\cdot100+13-0,2.2=212,6g\\ C_{\%ZnCl_2}=\dfrac{27,2}{212,6}\cdot100=12,79\%\)
9 tháng 11 2021
Bài 1: hình 2:
áp dụng HTL ta có: \(BH.BC=AB^2\Rightarrow20x=144\Rightarrow x=\dfrac{36}{5}\)
\(x+y=BC\Rightarrow\dfrac{36}{5}+y=20\Rightarrow y=\dfrac{64}{5}\)
Bài 2:
hình 4:
BC=BH+HC=1+4=5
áp dụng HTL ta có: \(BH.BC=AB^2\Rightarrow1.5=AB^2\Rightarrow x=\sqrt{5}\)
áp dụng HTL ta có: \(HC.BC=AC^2\Rightarrow4.5=AC^2\Rightarrow y=2\sqrt{5}\)
hình 6:
Áp dụng HTL ta có: \(BH.HC=AH^2\Rightarrow4x=25\Rightarrow x=\dfrac{25}{4}\)
MP
1
15 tháng 12 2023
Bài IV:
1: Xét tứ giác MAOB có
\(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
=>MAOB là tứ giác nội tiếp
=>M,A,O,B cùng thuộc một đường tròn
2: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của AB(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1) và (2) suy ra MO là đường trung trực của BA
=>MO\(\perp\)AB tại H và H là trung điểm của AB
Xét ΔMAO vuông tại A có AH là đường cao
nên \(MH\cdot MO=MA^2\left(3\right)\)
Xét (O) có
ΔACD nội tiếp
AD là đường kính
Do đó: ΔACD vuông tại C
=>AC\(\perp\)CD tại C
=>AC\(\perp\)DM tại C
Xét ΔADM vuông tại A có AC là đường cao
nên \(MC\cdot MD=MA^2\left(4\right)\)
Từ (3) và (4) suy ra \(MA^2=MH\cdot MO=MC\cdot MD\)
3: Ta có: \(\widehat{MAI}+\widehat{OAI}=\widehat{OAM}=90^0\)
\(\widehat{HAI}+\widehat{OIA}=90^0\)(ΔAHI vuông tại H)
mà \(\widehat{OAI}=\widehat{OIA}\)
nên \(\widehat{MAI}=\widehat{HAI}\)
=>AI là phân giác của góc HAM
Xét ΔAHM có AI là phân giác
nên \(\dfrac{HI}{IM}=\dfrac{AH}{AM}\left(5\right)\)
Xét ΔOHA vuông tại H và ΔOAM vuông tại A có
\(\widehat{HOA}\) chung
Do đó: ΔOHA đồng dạng với ΔOAM
=>\(\dfrac{OH}{OA}=\dfrac{HA}{AM}\)
=>\(\dfrac{OH}{OI}=\dfrac{AH}{AM}\left(6\right)\)
Từ (5) và (6) suy ra \(\dfrac{OH}{OI}=\dfrac{IH}{IM}\)
=>\(HO\cdot IM=IO\cdot IH\)
G
làm giúp em bài 1.58 nhớ là hình bài 1.58 là hình trên ko phải hình dưới
0
TL
1
HJ
1
2 tháng 10 2021
Bài 10:
a: \(\overrightarrow{AB}+\overrightarrow{BO}+\overrightarrow{OA}\)
\(=\overrightarrow{AO}+\overrightarrow{OA}=\overrightarrow{0}\)
b: \(\overrightarrow{OA}+\overrightarrow{BC}+\overrightarrow{DO}+\overrightarrow{CD}\)
\(=\overrightarrow{OA}+\overrightarrow{DO}+\overrightarrow{BD}\)
\(=\overrightarrow{OA}+\overrightarrow{BO}=\overrightarrow{BA}\)
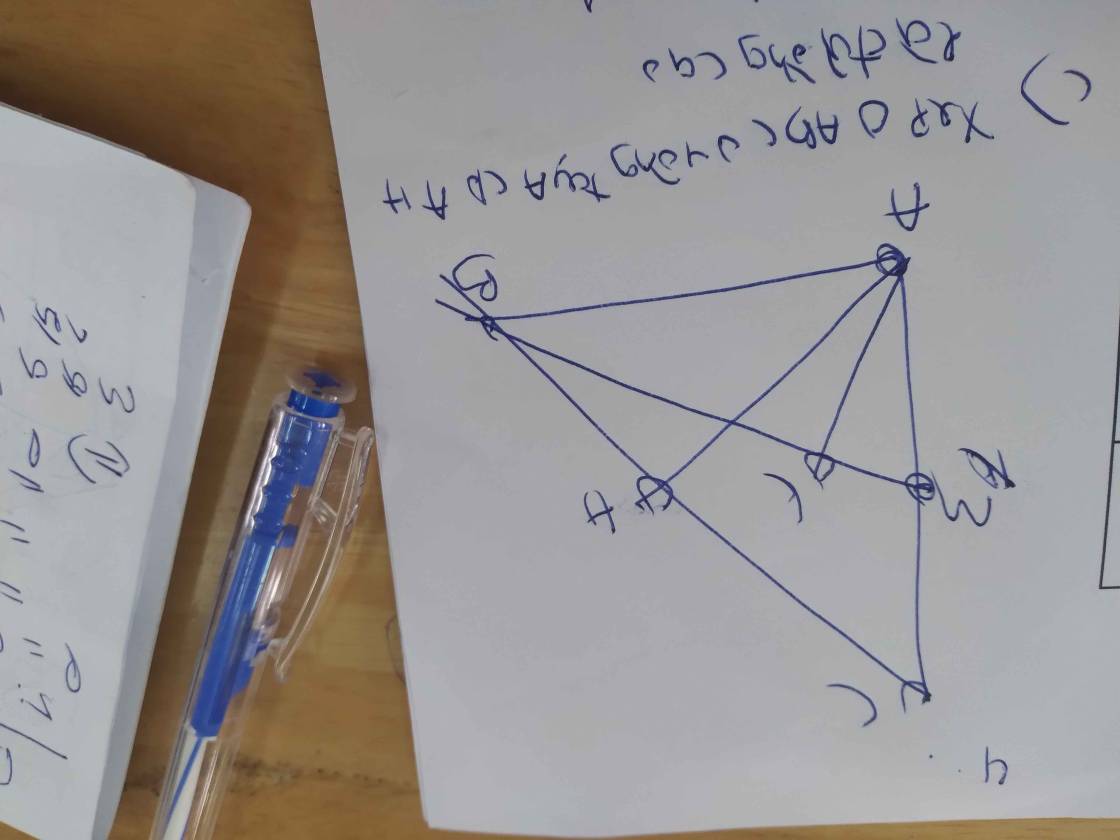
Bẹn tự vẽ hình nhé
1) Ta có: BOC=90 => CON+BON=90
Vì MON =90 (gt)
=> BOM+BON=90 => BOM=CON
+) BD là đường chéo=> BD là phân giác ABC => MBO=CBO = 1/2 BOC=45
Tương tự: NCO=DCO=1/2 BOC=45
=> MBO=NCO
Xét tam giác OBM và OCN có:
OB=OC
BOM=CON
MBO=NCO
=> Tam giác OBM=OCN (g.c.g)
=> OM=ON (1)
Lại có: MON =90(gt) (2)
Từ 1,2 => tam giác MON vuông cân (đpcm)
2) tam giác OBM= tam giác OCN(theo 1)
=> BM=CN
Mà AB=AC ( tứ giác ABCD là hình vuông)
=>AB-BM=BC-CN
=> AM=BM=AM/MB=BN/CN
Ta có: AB//CD (ABCD là hv) => AM//CE => AN/NE=BN/NC
=> AM/BM=AN/NE => MN//BE ( Ta-lét đảo)
3) Vì MN//BE (Theo 2) => BKN=MNO =45 (hai góc đồng vị, tam giác MON vuông cân)
=> tam giác BNK đồng dạng ONC ( BNK=ONK;BKN=OCN=45)
=> NB/NK=NO/NC
Xét tam giác BON và KNC có:
BNO=CNK
NB/NK=NO/NC
=> TAM GIÁC BON đồng dạng tam giác KNC( cgc)
=> NKC=NBO=45
=> BKC=BKN+CKN=90=> CK vuông góc BE (đpcm)
4) Vì KH//OM
Mà MK vuông góc OK
=> Mk vuôg góc KH
=> NKH=90
Lại có: NKC=45=> CKH=45=>BKN=NKC=CKH=45
Xét tam giác BKC có: BKN=NKC => KN là phân giác
Mà KH vuôg góc KN
=> KH là phân giác ngoài tam giác BKC => KC/KB=HC/HB
CMTT: KN/KH=BN/BH
=> KC/KB+KN/KH+NC/BH=HC/HB+BN/BH+CN/BH=BH/BH=1(ĐPCM)