1. Bài toán về Phân số
Câu hỏi: Rút gọn rồi tính giá trị biểu thức: A=2515+14−7+−1812
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LT
7 tháng 6 2021
ĐK: \(\left\{{}\begin{matrix}x-2\sqrt{x}-3\ne0\\\sqrt{x}+1\ne0\\3-\sqrt{x}\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)\ne0\\\sqrt{x}+1\ne0\left(hiển-nhiên\right)\\x\ne\sqrt{3}\end{matrix}\right.\)
\(\Leftrightarrow x\ne\sqrt{3}\)
\(P=\dfrac{x\sqrt{x}-3}{x-2\sqrt[]{x}-3}-\dfrac{2\left(\sqrt{x-3}\right)}{\sqrt{x}+1}+\dfrac{\sqrt{x}+3}{3-\sqrt{x}}\)
\(\Leftrightarrow\dfrac{x\sqrt{x}-3}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}-\dfrac{2\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}+\dfrac{\left(-\sqrt{x}-3\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-3\right)}\)
\(\Leftrightarrow\dfrac{x\sqrt{x}-3-2\left(x-9\right)-x-\sqrt{x}-3\sqrt{x}-3}{\left(\sqrt{x+1}\right)\left(\sqrt{x}-3\right)}\)
\(\Leftrightarrow\dfrac{\left(x-4\right)\sqrt{x}-3x+12}{\left(\sqrt{x+1}\right)\left(\sqrt{x}-3\right)}\)
Chúc bạn học tốt ^^
LT
7 tháng 6 2021
Không thấy câu b =))
\(x=14-6\sqrt{5}=\left(3+\sqrt{5}\right)^2\)
\(\Rightarrow\sqrt{x}=3+\sqrt{5}\)
Thay vào ta được
\(\dfrac{14-6\sqrt{5}-3\left(14-6\sqrt{5}\right)+12}{\left(3+\sqrt{5}+1\right)\left(3+\sqrt{5}-3\right)}\)
\(=\dfrac{12\sqrt{5}-16}{\left(4+\sqrt{5}\right)\sqrt{5}}=\dfrac{12\sqrt{5}-16}{4\sqrt{5}+5}\)
TB
1
11 tháng 12 2023
d: \(D=x^3-6x^2+12x-100\)
\(=x^3-6x^2+12x-8-92\)
\(=\left(x-2\right)^3-92\)
Khi x=-98 thì \(D=\left(-98-2\right)^3-92=-1000000-92=-1000092\)
e: \(E=\left(x+1\right)^3+6\left(x+1\right)^2+12x+20\)
\(=\left(x+1\right)^3+6\left(x+1\right)^2+12\left(x+1\right)+8\)
\(=\left(x+1+2\right)^3\)
\(=\left(x+3\right)^3\)
Khi x=5 thì \(E=\left(5+3\right)^3=8^3=512\)
f: \(F=\left(2x-1\right)\left(4x^2+2x+1\right)-7\left(x^3+1\right)\)
\(=\left(2x\right)^3-1^3-7x^3-7\)
\(=x^3-8\)
Khi x=-1/2 thì \(F=\left(-\dfrac{1}{2}\right)^3-8=-\dfrac{1}{8}-8=-\dfrac{65}{8}\)
g: \(G=\left(-x-2\right)^3+\left(2x-4\right)\left(x^2+2x+4\right)-x^2\left(x-6\right)\)
\(=-\left(x+2\right)^3+2\left(x-2\right)\left(x^2+2x+4\right)-x^3+6x^2\)
\(=-x^3-6x^2-12x-8+2\left(x^3-8\right)-x^3+6x^2\)
\(=-2x^3-12x-8+2x^3-16=-12x-24\)
Khi x=-2 thì \(G=-12\cdot\left(-2\right)-24=24-24=0\)
h: \(H=\left(x-1\right)^3-\left(x+2\right)\left(x^2-2x+4\right)+3\left(x+4\right)\left(x-4\right)\)
\(=x^3-3x^2+3x-1-\left(x^3+8\right)+3\left(x^2-16\right)\)
\(=x^3-3x^2+3x-1-x^3-8+3x^2-48\)
\(=3x-57\)
Khi x=-1/2 thì \(H=3\cdot\dfrac{-1}{2}-57=-1,5-57=-58,5\)
P
28 tháng 7 2023
Sửa: \(A=\left(3x+2\right)^2+\left(2x-7\right)^2-2\left(3x+2\right)\left(2x-7\right)\)
\(A=\left(3x+2\right)^2-2\left(3x+2\right)\left(2x-7\right)+\left(2x-7\right)^2\)
\(A=\left[\left(3x+2\right)-\left(2x-7\right)\right]^2\)
\(A=\left(3x+2-2x+7\right)^2\)
\(A=\left(x+9\right)^2\)
Thay \(x=-19\) vào A ta có:
\(A=\left(-19+9\right)^2=\left(-10\right)^2=100\)
Vậy: ...
LV
1
19 tháng 8 2023
\(A=\dfrac{4x+8-3x+6}{\left(x-2\right)\left(x+2\right)}\cdot\dfrac{x^2}{x+14}\)
\(=\dfrac{x+14}{x+14}\cdot\dfrac{x^2}{x^2-4}=\dfrac{x^2}{x^2-4}\)
Khi x=-3 thì \(A=\dfrac{\left(-3\right)^2}{\left(-3\right)^2-4}=\dfrac{9}{5}\)
T
22 tháng 12 2023
a) ĐKXĐ: \(x\ne0;x\ne-2\)
b) \(S=\dfrac{\left(x+2\right)^2}{x}\cdot\left(1-\dfrac{x^2}{x+2}\right)-\dfrac{x^2+6x+4}{x}\)
\(=\dfrac{\left(x+2\right)^2}{x}\cdot\dfrac{x+2-x^2}{x+2}-\dfrac{x^2+6x+4}{x}\)
\(=\dfrac{\left(x+2\right)\left(x+2-x^2\right)}{x}-\dfrac{x^2+6x+4}{x}\)
\(=\dfrac{x^2+2x-x^3+2x+4-2x^2-x^2-6x-4}{x}\)
\(=\dfrac{-x^3-2x^2-2x}{x}\)
\(=\dfrac{x\left(-x^2-2x-2\right)}{x}\)
\(=-x^2-2x-2\)
Với \(x=0\Rightarrow\) loại
Với \(x=1\), thay vào \(S\) ta được
\(S=-1^2-2\cdot1-2=-5\)
c) Có: \(S=-x^2-2x-2\)
\(=-\left(x^2+2x+2\right)\)
\(=-\left(x^2+2x+1\right)-1\)
\(=-\left(x+1\right)^2-1\)
Ta thấy: \(\left(x+1\right)^2\ge0\forall x\ne0;x\ne-2\)
\(\Rightarrow-\left(x+1\right)^2\le0\forall x\ne0;x\ne-2\)
\(\Rightarrow S=-\left(x+1\right)^2-1\le-1\forall x\ne0;x\ne-2\)
Dấu \("="\) xảy ra khi: \(x+1=0\Leftrightarrow x=-1\left(tmdk\right)\)
\(\text{#}\mathit{Toru}\)
M
2
P
14 tháng 8 2023
\(P=\dfrac{x^2-1}{x+5}\cdot\dfrac{2x+10}{x^2-x}\) (ĐK: \(x\ne-1,x\ne0,x\ne1\))
\(P=\dfrac{\left(x-1\right)\left(x+1\right)}{x+5}\cdot\dfrac{2\left(x+5\right)}{x\left(x-1\right)}\)
\(P=\dfrac{2\left(x-1\right)\left(x+1\right)\left(x+5\right)}{x\left(x+5\right)\left(x-1\right)}\)
\(P=\dfrac{2\left(x+1\right)}{x}\)
Thay \(x=99\left(tm\right)\) vào P ta có:
\(P=\dfrac{2\left(99+1\right)}{99}=\dfrac{2\cdot100}{99}=\dfrac{200}{99}\)
14 tháng 8 2023
\(P=\dfrac{x^2-1}{x+5}\cdot\dfrac{2x+10}{x^2-x}\\ =\dfrac{\left(x^2-1\right)\left(2x+10\right)}{\left(x+5\right)\left(x^2-x\right)}\\ =\dfrac{\left(x+1\right)\left(x-1\right)\left(x+5\right)2}{\left(x+5\right)\left(x-1\right)x}\\ =\dfrac{2x+2}{x}\)
Thay \(x=99\) vào P ta có
\(P=\dfrac{2.99+2}{99}\\ =\dfrac{200}{99}\)
Vậy \(x=99\) thì \(P=\)\(\dfrac{200}{99}\)
CM
22 tháng 1 2017
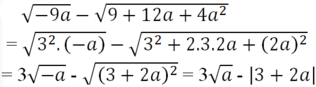
Tại a = -9 ta được:
= 3√-(-9) - |3 + 2(-9)|
= 3√32 - |3 - 18|
= 3.3 - |-15| = 9 - 15 = -6
Tuyệt vời! Dưới đây là một số câu hỏi toán lớp 6 kèm theo đáp án
Để tính giá trị biểu thức A, chúng ta cần rút gọn từng phân số trước, sau đó thực hiện phép cộng các phân số đã rút gọn.
A=3018+30−15+30−20 A=3018+(−15)+(−20) A=303+(−20) A=30−17
Đáp số: A=−3017
A = 2515 + 14 - 7 - 1812
A = 2515 + 14 - 7 - 1812
A = 2529 - 7 - 1872
A = 2522 - 1872
A = 650