Tìm số a để đa thức 10x2- 7x+ a chia hết cho đa thức 2x- 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: =>2x^3-4x^2-3x^2+6x+4x-8+a+8 chia hết cho x-2
=>a+8=0
=>a=-8
b: =>2x^3+x^2-x^2-0,5x-0,5x+0,25+m-0,25 chia hết cho 2x+1
=>m-0,25=0
=>m=0,25

Ta thực hiện phép chia 10x2- 7x+ a cho 2x- 3
thì đc 5x+ 4 và dư a+ 12. Muốn đa thức 10x2- 7x+ a chia hết cho đa thức 2x- 3
thì a+ 12 phải =0 suy ra a = -12

3x^3 + 2x^2 - 7x + a 3x - 1 x^2 + x - 2 3x^3 - x^2 3x^2 - 7x 3x^2 - x -6x + a -6x + 2 a - 2
Để : \(3x^3+2x^2-7x+a⋮3x-1\)<=> \(a-2=0\)
<=> \(a=2\)
Vậy a = 2
3x^3 + 3x^2 + 5x + a x + 3 3x^2 - 6x + 22 3x^3 + 9x^2 -6x^2 + 5x -6x^2 - 18x 22x + a 22x + 66
Để \(x^3+3x^2+5x+a⋮x+3\)<=> \(a-66=0\)
<=> \(a=66\)
Vậy a = 66

Ta thấy \(B=\left(x-1\right)\left(x-5\right)\) nên để đa thức A chia hết cho đa thức B thì \(A=\left(x-1\right)\left(x-5\right).C\) với \(C\) là một đa thức bậc 2 hệ số nguyên theo \(x\).
Điều này tương đương với việc \(A\) có 2 nghiệm là \(x=1,x=5\). Do đó \(A\left(1\right)=0\) \(\Leftrightarrow1^4-7.1^3+10.1^2+\left(a-1\right)+b-a=0\) \(\Leftrightarrow b=-3\)
Ta viết lại \(A=x^4-7x^3+10x^2+\left(a-1\right)x-3-a\). Ta có \(A\left(5\right)=0\) \(\Leftrightarrow5^4-7.5^3+10.5^2+\left(a-1\right).5-3-a=0\) \(\Leftrightarrow4a-8=0\) \(\Leftrightarrow a=2\).
Vậy để đa thức A chia hết cho đa thức B thì \(a=2,b=-3\).
A:B=x2-x+11 dư (a+70)x+b-a-55
Để A chia hết cho B thì
(a+70)x+b-a-55=0
b-a-55=0 (a khác -70) tại x=0
Vậy b-a=55 thỏa đề bài

a) f(x) = 10x² - 7x - 5 = 10x² - 15x + 8x - 12 + 7 = 5x(2x-3) + 4(2x-3) + 7
f(x) chia hết cho 2x-3 khi và chỉ khi 7 chia hết cho 2x-3, vì 7 là số nguyên tố, nên chi có các trường hợp:
TH1: 2x-3 = -1 <=> x = 1
TH2: 2x-3 = 1 <=> x = 2
TH3: 2x-3 = -7 <=> x = -2
TH4: 2x-3 = 7 <=> x = 5
Vây có 4 giá trị nguyên của x là {-2, 1, 2, 5}
a) f(x) = 10x² - 7x - 5 = 10x² - 15x + 8x - 12 + 7 = 5x(2x-3) + 4(2x-3) + 7
f(x) chia hết cho 2x-3 khi và chỉ khi 7 chia hết cho 2x-3, vì 7 là số nguyên tố, nên chi có các trường hợp:
TH1: 2x-3 = -1 <=> x = 1
TH2: 2x-3 = 1 <=> x = 2
TH3: 2x-3 = -7 <=> x = -2
TH4: 2x-3 = 7 <=> x = 5
Vây có 4 giá trị nguyên của x là {-2, 1, 2, 5}
b) g(x) = x³ - 4x² + 5x - 1 = x³ - 3x² - x² + 3x + 2x - 6 + 5 = x²(x-3) - x(x-3) + 2(x-3) + 5
g(x) chia hết cho x-3 khi và chỉ khi 5 chia hết cho x-3 (5 là số nguyên tố nên chỉ xét các trường hợp)
TH1: x-3 = -5 <=> x = -2
TH2: x-3 = -1 <=> x = 2
TH3: x-3 = 1 <=> x = 4
TH4: x-3 = 5 <=> x = 8
Vậy có giá trị nguyên của x thỏa là {-1, 2, 4, 8}

a: 3x^3+2x^2-7x+a chia hêt cho 3x-1
=>3x^3-x^2+3x^2-x-6x+2+a-2 chia hết cho 3x-1
=>a-2=0
=>a=2
c: =>2x^2-6x+(a+6)x-3a-18+3a+19 chia x-3 dư 4
=>3a+19=4
=>3a=-15
=>a=-5
d: 2x^3-x^2+ax+b chiahêt cho x^2-1
=>2x^3-2x-x^2+1+(a+2)x+b-1 chia hết cho x^2-1
=>a+2=0 và b-1=0
=>a=-2 và b=1

\(a,A=\left(x^2-4xy+4y^2\right)+10\left(x-2y\right)+25+\left(y^2-2y+1\right)+2\\ A=\left(x-2y\right)^2+10\left(x-2y\right)+5+\left(y-1\right)^2+2\\ A=\left(x-2y+5\right)^2+\left(y-1\right)^2+2\ge2\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=2y-5\\y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=1\end{matrix}\right.\)
\(b,\Leftrightarrow3x^3+10x^2-5+n=\left(3x+1\right)\cdot a\left(x\right)\)
Thay \(x=-\dfrac{1}{3}\Leftrightarrow3\left(-\dfrac{1}{27}\right)+10\cdot\dfrac{1}{9}-5+n=0\)
\(\Leftrightarrow-\dfrac{1}{9}+\dfrac{10}{9}-5+n=0\\ \Leftrightarrow-4+n=0\Leftrightarrow n=4\)
\(c,\Leftrightarrow2n^2-4n+5n-10+3⋮n-2\\ \Leftrightarrow2n\left(n-2\right)+5\left(n-2\right)+3⋮n-2\\ \Leftrightarrow n-2\inƯ\left(3\right)=\left\{-3;-1;1;3\right\}\\ \Leftrightarrow n\in\left\{-1;1;3;5\right\}\)
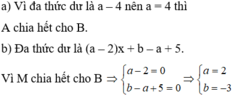
Vì (10x2-7x+a):(2x-3)=5x+4 dư a+12 nên để 10x2-7x+a chia hết cho 2x-3 thì a+12=0=> a=-12
Đặt tính chia hai đa thức, ta được: \(\left(10x^2-7x+a\right):\left(2x-3\right)=5x+4\) (dư a - -12)
Để đa thức \(10x^2-7x+a\) chia hết cho đa thức \(2x-3\) thì a + 12 = 0 => a = 0 - 12 = -12
Vậy a = -12