giúp mình với ạ, mình cảm ơn nhiều lắm ạ!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 9 2018
Xét phương trình hoành độ giao điểm của parabol (P) và đường thẳng d
5x2 = −4x – 4 ⇔ 5x2 + 4x + 4 = 0
⇔ 4x2 + x2 + 4x + 4 = 0
⇔ x2 + (x + 2)2 = 0(*)
Xét x2 + (x + 2)2 ≥ 0; ∀ x và dấu “=” xảy ra khi
x = 0 x + 2 = 0 ⇔ x = 0 x = − 2 (vô lý)
nên x2 + (x + 2)2> 0, ∀ x
Hay phương trình (*) vô nghiệm
Vậy không có giao điểm của đường thẳng (d) và parabol (P)
Đáp án cần chọn là: B
CM
6 tháng 12 2019
Xét phương trình hoành độ giao điểm của parabol (P) và đường thẳng d
2x2 = x + 1 ⇔ 2x2 – x – 1 = 0 ⇔ 2x2 – 2x + x – 1 = 0
⇔ 2x(x – 1) + (x− 1) = 0
⇔ (2x + 1) (x – 1) = 0
⇔ x = − 1 2 x = 1
Vậy có hai giao điểm của đường thẳng d và parabol (P)
Đáp án cần chọn là: D
5 tháng 5 2021
b) Phương trình hoành độ giao điểm của (P) và (d) là:
\(x^2=2\left(m-1\right)x+5-2m\)
\(\Leftrightarrow x^2-2\left(m-1\right)x-5+2m=0\)
Áp dụng hệ thức Vi-et, ta được:
\(x_1+x_2=2\left(m-1\right)\)
Ta có: \(x_1+x_2=6\)
\(\Leftrightarrow2\left(m-1\right)=6\)
\(\Leftrightarrow m-1=3\)
hay m=4
Vậy: m=4
2 tháng 4 2016
Mỗi đườg thẳng cắt 2005 đường thẳng còn lại tạo nên 2005 giao điểm .
Mà có 2006 đường thẳng => có : 2005.2006 giao điểm . Nhưng mỗi giao điểm được tính 2 lần => so giao diem thuc te la :
(2005 x 2006) : 2 = 1003 x 2005 = 2011015 giao điểm
12 tháng 5 2023
b: PTHĐGĐ là:
-1/2x^2=1/2x-1
=>-x^2=x-2
=>-x^2-x+2=0
=>x^2+x-2=0
=>x=-2 hoặc x=1
=>y=-1/2*4=-2 hoặc y=-1/2
a: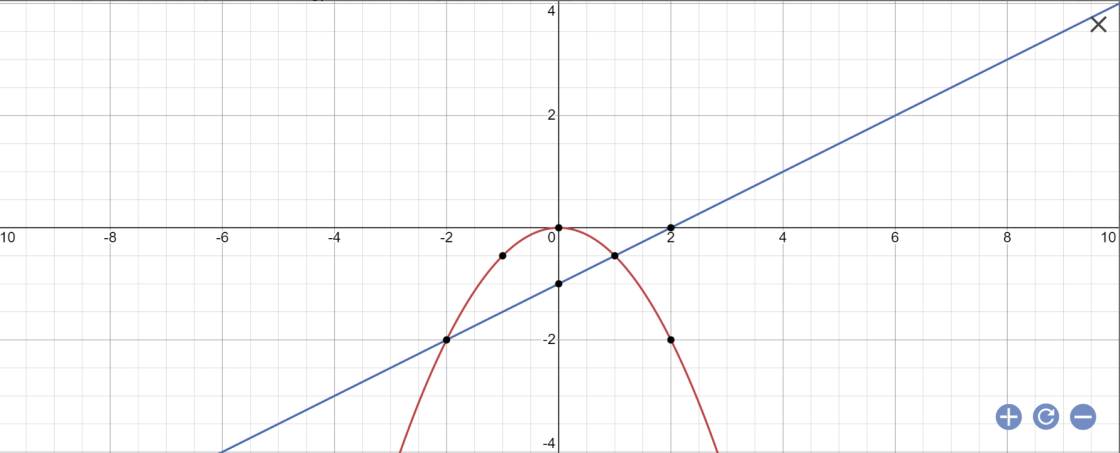 
NA
Nguyễn An Ninh
VIP
12 tháng 5 2023
b. ta có phương trình hoành độ: 1/2.x^2=3/2.x-1 <=>1/2.x^2-3/2.x+1=0 <=> x^2-3x+2=0
Δ=1>0 =>pt có hai nghiệm phân biệt
x=2 =>y=2 =>A (2;2)
x=1 =>y=1/2 =>B(1;1/2)
Vậy (P)và (d) cắt nhau tại hai điểm A(2;2) và B(1;1/2)
26 tháng 3 2022
Hoành độ giao điểm tm pt
\(x^2-3x+2=0\Leftrightarrow x=1;x=2\)
\(\Rightarrow y=1;y=4\)
Vậy (P) cắt (d) tại A(1;1) ; B(2;4)
12 tháng 3 2020
a) Thay tọa dộ của điểm T vào dg thẳng d ta dc: -2.(-2) - 6 = -2 (Thỏa mãn)
Vậy điểm T có thuộc dg thẳng d
b) Pt hoành độ giao điểm của (d) và (P) là: -8x2 = -2x - 6
<=> 8x2 - 2x - 6 = 0
<=> (x - 1)(8x + 6) = 0 <=> \(\orbr{\begin{cases}x=1\\x=-\frac{3}{4}\end{cases}}\)
* Với x = 1 => y = -8
* Với x = -3/4 => y = -9/2
Tự kết luận nha
9 tháng 6 2021
a) Khi \(m=1\) \(\Rightarrow\left(d\right):y=2x+8\)
Xét phương trình hoành độ giao điểm
\(x^2=2x+8\) \(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-2\end{matrix}\right.\)
+) Với \(x=4\Rightarrow y=16\)
+) Với \(x=-2\Rightarrow y=4\)
Vậy khi \(m=1\) thì (P) cắt (d) tại 2 điểm phân biệt \(\left(4;16\right)\) và \(\left(-2;4\right)\)
b) Xét phương trình hoành độ giao điểm
\(x^2-2x+m^2-9=0\) (*)
Ta có: \(\Delta'=10-m^2\)
Để (P) cắt (d) \(\Leftrightarrow\) Phương trình (*) có 2 nghiệm phân biệt
\(\Leftrightarrow\Delta'=10-m^2>0\) \(\Leftrightarrow-\sqrt{10}< m< \sqrt{10}\)
Theo đề: (P) cắt (d) tại 2 điểm nằm về 2 phía của trục tung
\(\Leftrightarrow\) Phương trình (*) có 2 nghiệm trái dấu
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta'>0\\x_1x_2< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}10-m^2>0\\m^2-9< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-\sqrt{10}< m< \sqrt{10}\\-3< m< 3\end{matrix}\right.\) \(\Leftrightarrow-3< m< 3\)
Vậy ...
khi m thay đổi
x2 và đường thẳng (d) : y = mx - 
.
a: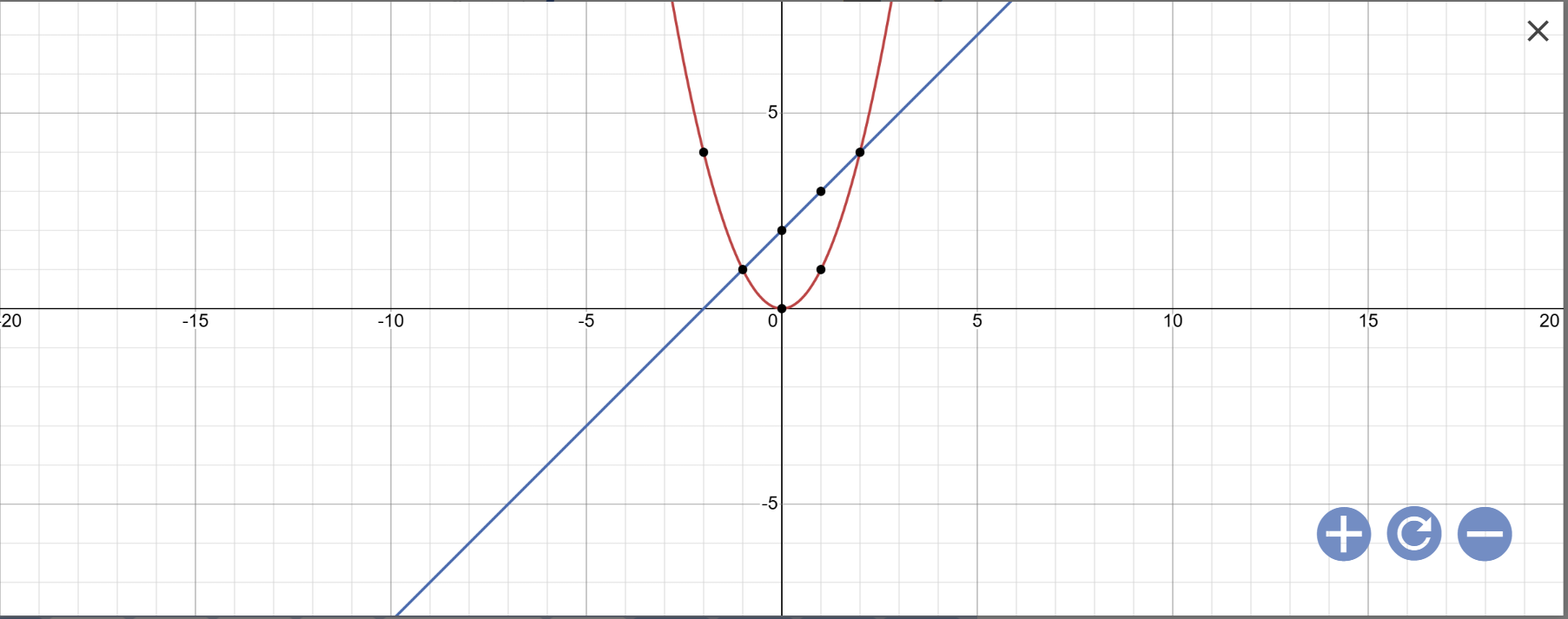
b: Phương trình hoành độ giao điểm là:
\(x^2=x+2\)
=>\(x^2-x-2=0\)
=>(x-2)(x+1)=0
=>\(\left[{}\begin{matrix}x-2=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
Khi x=2 thì y=x+2=2+2=4
Khi x=-1 thì y=-1+2=1
vậy: Tọa độ giao điểm của (P) và (d) là A(2;4); B(-1;1)
c: A,B là tọa độ các giao điểm của (d) và (P)
=>A(2;4); B(-1;1)
O(0;0); A(2;4); B(-1;1)
\(OA=\sqrt{\left(2-0\right)^2+\left(4-0\right)^2}=2\sqrt{5}\)
\(OB=\sqrt{\left(-1-0\right)^2+\left(1-0\right)^2}=\sqrt{2}\)
\(AB=\sqrt{\left(-1-2\right)^2+\left(1-4\right)^2}=3\sqrt{2}\)
Xét ΔOAB có \(BO^2+BA^2=OA^2\)
nên ΔBOA vuông tại B
=>\(S_{BOA}=\dfrac{1}{2}\cdot BA\cdot BO=\dfrac{1}{2}\cdot3\sqrt{2}\cdot\sqrt{2}=3\)