Cho biểu thức $P=\Big(\dfrac{x-2}{x+2\sqrt{x}}+\dfrac{1}{\sqrt{x}+2}\Big).\dfrac{\sqrt{x}+1}{\sqrt{x}-1}$ với $x>0, \, x \ne 1$.
a) Chứng minh $P=\dfrac{\sqrt{x}+1}{\sqrt{x}}$.
b) Tìm $x$ để $2P=2\sqrt{x}+5$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

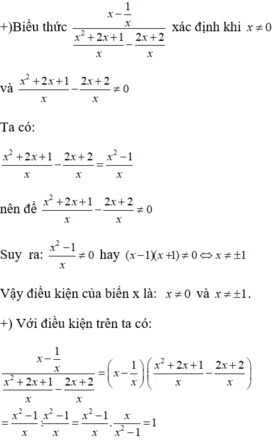
Vậy với điều kiện x ≠ 0 và x ≠ ± 1 thì biểu thức đã cho không phụ thuộc biến x.
bạn ơi cho mik hỏi sao x^2+2x+1/x -2x+2/x lại bàng x^2-1/x thế ak

Ta có![]() xác định khi x + 1
≠
0 và x – 1
≠
0 ⇒ x
≠
±
1
xác định khi x + 1
≠
0 và x – 1
≠
0 ⇒ x
≠
±
1
![]() xác định khi x – 1 ≠ 0 và x2 – 1
≠
0 ⇒ x
≠
±
1
xác định khi x – 1 ≠ 0 và x2 – 1
≠
0 ⇒ x
≠
±
1
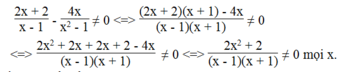
Vậy điều kiện để biểu thức xác định x ≠ ± 1
Ta có
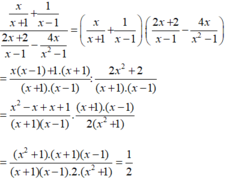
Vậy với x ≠ ± 1 thì biểu thức đã cho không phụ thuộc vào x.

Biểu thức xác định khi x 2 - 36 ≠ 0 , x 2 + 6 x ≠ 0 , 6 – x ≠ 0 và 2x – 6 ≠ 0
x 2 - 36 ≠ 0 ⇒ (x – 6)(x + 6) ≠ 0 ⇒ x ≠ 6 và x ≠ -6
x 2 + 6 x ≠ 0 ⇒ x(x + 6) ≠ 0 ⇒ x ≠ 0 và x ≠ -6
6 – x ≠ 0 ⇒ x ≠ 6
2x – 6 ≠ 0 ⇒ x ≠ 3
Vậy x ≠ 0, x ≠ 3, x ≠ 6 và x ≠ -6 thì biểu thức xác định.
Ta có:
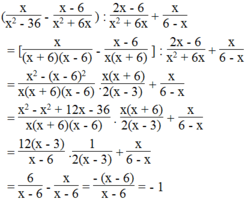
Vậy biểu thức không phụ thuộc vào biến x.

Biểu thức xác định khi x – 1 ≠ 0, x 2 - 2 x + 1 ≠ 0 và x 2 - 1 ≠ 0
x – 1 ≠ 0 ⇒ x ≠ 1
x 2 - 2 x + 1 ≠ 0 ⇒ x - 1 2 ≠ 0 ⇒ x ≠ 1
x 2 - 1 ≠ 0 ⇒ (x – 1)(x + 1) ≠ 0 ⇒ x ≠ -1 và x ≠ 1
Vậy biểu thức xác định với x ≠ -1 và x ≠ 1
Ta có:
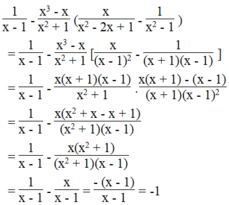
Vậy biểu thức không phụ thuộc vào biến x.

a) Ta có: x4 - 1 = (x2 + 1)(x2-1), trong đó : x2 + 1 > 0, với mọi x.
Vậy điều kiện : x2 – 1 ≠ 0
x2 – 1 = (x – 1)(x + 1) ≠ 0 ⇒ x ≠ ±1
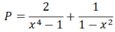
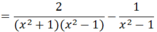
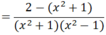
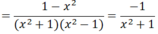
Do x2 + 1 > 0 với mọi x nên P < 0 với mọi x ≠ ±1

a) \(P=\left(\frac{\sqrt{x}}{\sqrt{x}-2}+\frac{1}{\sqrt{x}+2}-\frac{2}{4-x}\right):\frac{\sqrt{x}+3}{\sqrt{x}-2}\left(ĐK:x\ge0;x\ne4\right)\)
\(=\frac{\sqrt{x}\left(\sqrt{x}+2\right)+\sqrt{x}-2+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\frac{\sqrt{x}-2}{\sqrt{x}+3}\)
\(=\frac{x+2\sqrt{x}+\sqrt{x}}{\sqrt{x}+2}\cdot\frac{1}{\sqrt{x}+3}\)
\(=\frac{\sqrt{x}\left(\sqrt{x}+3\right)}{\sqrt{x}+2}\cdot\frac{1}{\sqrt{x}+3}=\frac{\sqrt{x}}{\sqrt{x}+2}\)
b) Vì: \(\sqrt{x}+4>0,\forall x\inĐK\)
=> \(2\sqrt{x}+4>\sqrt{x}\)
=> \(\frac{\sqrt{x}}{2\sqrt{x}+4}< 0\)
=> \(\frac{\sqrt{x}}{\sqrt{x}+2}< 2\)
=>đpcm

![]() xác định khi:
xác định khi:
(x + y)(6x – 6y)
≠
0 ⇒ 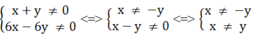
Điều kiện x ≠ ± y
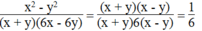
Vậy biểu thức không phụ thuộc vào x, y.
a: \(P=\left(\dfrac{x-2}{x+2\sqrt{x}}+\dfrac{1}{\sqrt{x}+2}\right)\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
\(=\left(\dfrac{x-2}{\sqrt{x}\left(\sqrt{x}+2\right)}+\dfrac{1}{\sqrt{x}+2}\right)\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
\(=\dfrac{x+\sqrt{x}-2}{\left(\sqrt{x}+2\right)\cdot\sqrt{x}}\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
\(=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}+1}{\sqrt{x}}=\dfrac{\sqrt{x}+1}{\sqrt{x}}\)
b: \(2P=2\sqrt{x}+5\)
=>\(2\left(\sqrt{x}+1\right)=\sqrt{x}\left(2\sqrt{x}+5\right)\)
=>\(2x+5\sqrt{x}-2\sqrt{x}-2=0\)
=>\(2x+3\sqrt{x}-2=0\)
=>\(\left(\sqrt{x}+2\right)\left(2\sqrt{x}-1\right)=0\)
mà \(\sqrt{x}+2>=2>0\forall x\) thỏa mãn ĐKXĐ
nên \(2\sqrt{x}-1=0\)
=>\(\sqrt{x}=\dfrac{1}{2}\)
=>\(x=\dfrac{1}{4}\left(nhận\right)\)