Cách tính chiều cao trong một tam giác đều
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 8 2023
5:
HB=căn AB^2-AH^2=5cm
AC=căn AH^2+HC^2=20cm
BC=HB+HC=5+16=21cm
CM
26 tháng 10 2017
Chọn C.
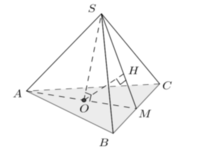
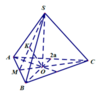
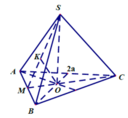
- Gọi O là trọng tâm của tam giác ABC và M là trung điểm của BC.
- Vì hình chóp S.ABC là hình chóp tam giác đều nên: S) ⊥ (ABC); SO = a√3.
- Kẻ OH ⊥ SM, ta có:
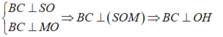nên suy ra d(O; (SBC)) = OH.
- Ta có:
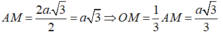
- Xét tam giác vuông SOM, đường cao OH có:
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
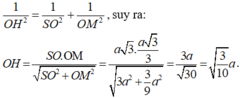
a) Gọi E là trung điểm của AD
\(\left( {SAD} \right) \bot \left( {ABCD} \right),\left( {SAD} \right) \cap \left( {ABCD} \right) = AD\)
Mà tam giác SAD đều
\( \Rightarrow \) \(SE \bot \left( {ABCD} \right)\)
Xét tam giác SDE vuông tại E có
\(SE = \sqrt {S{D^2} - D{E^2}} = \sqrt {{a^2} - {{\left( {\frac{a}{2}} \right)}^2}} = \frac{{a\sqrt 3 }}{2}\)
b) Ta có \(AB \bot AD,AB \bot SE\left( {SE \bot \left( {ABCD} \right)} \right) \Rightarrow AB \bot \left( {SAD} \right)\)
Vì BC // AD (ABCD là hình vuông), \(AD \subset \left( {SAD} \right)\) nên BC // (SAD)
\( \Rightarrow \) d(BC, (SAD)) = d(B, (SAD)) = AB = a
c) Trong (SAD) kẻ \(AF \bot SD\)
Có \(AB \bot \left( {SAD} \right),AF \subset \left( {SAD} \right) \Rightarrow AB \bot AF\)
\( \Rightarrow \) d(AB, SD) = AF
Vì tam giác SAD đều nên \(AF = SE = \frac{{a\sqrt 3 }}{2}\)
Vậy \(d\left( {AB,{\rm{ }}SD} \right) = \frac{{a\sqrt 3 }}{2}\)
23 tháng 12 2016
Gọi chiều cao hình tam giác là a => độ dài đáy hình tam giác là 2 x a
Theo bài ra , ta có :
S = 2 x a x a : 2 = 4
=> a x a = 4
<=> a x a = 2 x 2
=> a =2
Vậy chiều cao của hình tam giác đó là 2m = 20dm
12 tháng 2 2016
chiều cao hình tam giác ta lấy 2 lần diện tích chia cho đáy \(h=\frac{2xS}{a}\)
chiều cao hình thang ta lấy tổng 2 lần diện tích chia cho tổng 2 đáy h = 2 x S : ( a + b )
ủng hộ cho mình lên 200 nha
12 tháng 2 2016
chiều cao hình TG: diện tích nhân 2 chia đọ dài đáy
chiều cao hình thang: diện tính nhân 2 chia tổng độ dài 2 đáy
(hình như là thế, mik c~ ko nhớ rõ nữa ^^ )
26 tháng 3 2022
a. chiều cao của tam giác là: \(\approx10,06\)
b. tớ chưa biết
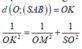
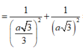
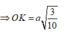
h = a√3/2 (a là chiều dài cạnh trong tam giác).