Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi \(I\) là trung điểm của \(BC\), kẻ \(OH \bot SI\left( {H \in SI} \right)\).
\(ABC\) là tam giác đều \( \Rightarrow AI \bot BC\)
\(SO \bot \left( {ABC} \right) \Rightarrow SO \bot BC\)
\( \Rightarrow BC \bot \left( {SAI} \right) \Rightarrow BC \bot OH\)
Mà \(OH \bot SI\)
\( \Rightarrow OH \bot \left( {SBC} \right) \Rightarrow d\left( {O,\left( {SBC} \right)} \right) = OH\)
\(ABC\) là tam giác đều \( \Rightarrow AI = \frac{{AB\sqrt 3 }}{2} = a\sqrt 3 \Rightarrow OI = \frac{1}{3}AI = \frac{{a\sqrt 3 }}{3}\)
\(SO = a\sqrt 2 \Rightarrow OH = \frac{{SO.OI}}{{\sqrt {S{O^2} + O{I^2}} }} = \frac{{a\sqrt {14} }}{7}\)
Chọn A.
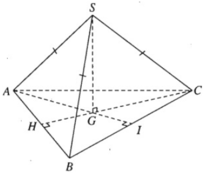
a) SG là trục đường tròn ngoại tiếp tam giác đều ABC nên SG ⊥ (ABC). Ta có
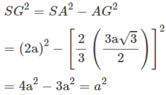
Vậy khoảng cách từ S tới mặt phẳng (ABC) là độ dài của đoạn SG = a
Ta có CG ⊥ AB tại H. Vì GH là đoạn vuông góc chung của AB và SG, do đó
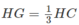
mà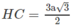 
nên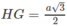 
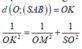
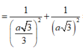
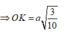
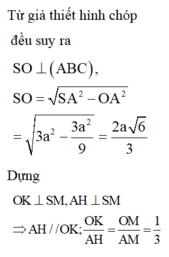
Tam giác SBC cân hay đều em nhỉ?
Vì tam giác SBC đều thì sẽ không khớp với dữ kiện \(V_{SABC}=\dfrac{a^3}{16}\)
Ta tính được \(AG=a\dfrac{\sqrt{3}}{3}\)
Từ gt ta có:
\(\widehat{\left(SA,\left(ABC\right)\right)}=\widehat{\left(SA,AG\right)}=\widehat{SAG}=60^0\)(Vì S.ABC là chóp tam giác đều nên \(SG\perp\left(ABC\right)\))
Khi đó SG=AG.tan60=a
Gọi M là trung điểm BC \(\Rightarrow GM=a\dfrac{\sqrt{3}}{6}\)
Đặt d(G,(SBC))=x
Áp dụng mô hình "điểm tốt - vẽ hai bước" cho hình chóp S.GBC với G là "điểm tốt" ta có:
\(\dfrac{1}{x^2}=\dfrac{1}{SG^2}+\dfrac{1}{GM^2}=\dfrac{1}{a^2}+\dfrac{1}{\left(a\dfrac{\sqrt{3}}{6}\right)^2}\)
\(\Rightarrow x=\dfrac{a}{\sqrt{13}}\)
Mô hình "điểm tốt - vẽ hai bước": Cho hình chóp S.ABC với \(SA\perp\left(ABC\right)\). Kẻ \(AH\perp BC,AK\perp SH\) thì d(A,(SBC))=AK.
CM: Ta có: \(SA\perp\left(ABC\right)\Rightarrow SA\perp AH\)
Mà \(AH\perp BC\Rightarrow BC\perp\left(SAH\right)\)
\(\Rightarrow\left(SBC\right)\perp\left(SAH\right)\) theo giao tuyến SH
Mà \(AK\perp SH,AK\subset\left(SAH\right)\) \(\Rightarrow AK\perp\left(SBC\right)\), dễ dàng suy ra đpcm
Chọn C.
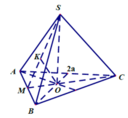
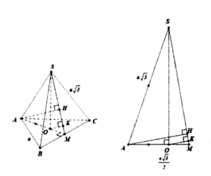
- Gọi O là trọng tâm của tam giác ABC và M là trung điểm của BC.
- Vì hình chóp S.ABC là hình chóp tam giác đều nên: S) ⊥ (ABC); SO = a√3.
- Kẻ OH ⊥ SM, ta có:
- Ta có:
- Xét tam giác vuông SOM, đường cao OH có: