(5x+1)^2=36/49 x-(2/9)^3=(2/3)^6
(8x)^2x+1=5^2x+1 x-(2,5)^2+(y-1/10)^2≤0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
29 tháng 8 2019
a) Ta có: 2. (-2) ≤ 3 nên -2 có là nghiệm của bất phương trình
+) 
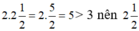không là nghiệm của bất phương trình ,
+) 2π > 3 nên π không là nghiệm của bất phương trình.
+) 
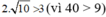nên √10 không là nghiệm của bất phương trình,
Các số là nghiệm của bất phương trình trên là: -2;
Các số không là nghiệm của bất phương trình trên là: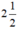 
; π; √10
b)2x ≤ 3 ⇔ x ≤ 3/2
Biểu diễn tập nghiệm trên trục số là:
23 tháng 7 2021
Bài 1:
a) Ta có: \(2\left(3-4x\right)=10-\left(2x-5\right)\)
\(\Leftrightarrow6-8x-10+2x-5=0\)
\(\Leftrightarrow-6x+11=0\)
\(\Leftrightarrow-6x=-11\)
hay \(x=\dfrac{11}{6}\)
b) Ta có: \(3\left(2-4x\right)=11-\left(3x-1\right)\)
\(\Leftrightarrow6-12x-11+3x-1=0\)
\(\Leftrightarrow-9x-6=0\)
\(\Leftrightarrow-9x=6\)
hay \(x=-\dfrac{2}{3}\)
. Ta có:
CM
9 tháng 3 2017
a) Sai lầm là coi -2 là hạng từ và chuyển vế hạng tử này trong khi -2 là một nhân tử.
Lời giải đúng:
-2x > 23
⇔ x < 23 : (-2) (chia cho số âm nên đổi chiều)
⇔ x < -11,5
Vậy nghiệm của bất phương trình là x < -11,5
b) Sai lầm là nhân hai vế của bất phương trình với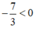 
mà không đổi chiều bất phương trình.
Lời giải đúng:
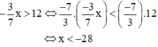
Vậy nghiệm của bất phương trình là x < -28
VT
26 tháng 4 2018
Phương trình của dao động điều hòa x= Acos(ωt + φ)
Trong đó :
- x : li độ của dao động (độ lệch của vật khỏi vị trí cân bằng) có đơn vị là centimet hoặc mét (cm ; m)
- A : biên độ dao động, có đơn vị là centimet hoặc mét (cm ; m)
- ω : tần số góc của dao động có đơn vị là radian trên giây (rad/s)
- (ωt + φ) : pha của dao động tại thời điểm t, có đơn vị là radian (rad)
- φ: pha ban đầu của dao động, có đơn vị là radian (rad)
LT
1 tháng 4 2017
Phương tridnh dao động điều hòa là x = Acos(ωt+ Ø), trong đó:
- x là li độ của dao động
- A là biên độ dao động
- ω là tần số góc của đơn vị, có đơn vị là rad/s
- (ωt+ Ø) là pha của dao động tại thời điểm t, có đơn vị là rad,
- Ø là pha ban đầu của dao động
CM
22 tháng 5 2018
Sử dụng tính chất “cộng hay trừ hai vế một bất đẳng thức với cùng một số và giữ nguyên chiều bất đẳng thức ta được một bất đẳng thức tương đương”.
Đáp án: A
5 tháng 3 2022
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x+7=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-7\end{matrix}\right.\)
24 tháng 7 2021
+ TH1: Xét x ≥ 5, khi đó x - 5 ≥ 0 nên |x – 5| = x – 5
⇔ x – 5 = 2x
⇔ x – 2x = 5
⇔ -x = 5
⇔ x = -5 < 5 (loại)
+ TH2: Xét x < 5, khi đó x - 5 < 0 nên |x – 5| = -(x – 5)
(3) ⇔ -(x – 5) = 2x
⇔ -x + 5 = 2x
⇔ -x - 2x = -5
⇔ -3x = -5
⇔x = \(\dfrac{5}{3}\)(thỏa mãn)
Vậy phương trình có tập nghiệm \(S=\left\{\dfrac{5}{3}\right\}\)
24 tháng 7 2021
Ta có: \(\left|x-5\right|=2x\)
\(\Leftrightarrow\left[{}\begin{matrix}x-5=2x\left(x\ge5\right)\\x-5=-2x\left(x< 5\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x-2x=5\\x+2x=5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-5\left(loại\right)\\x=\dfrac{5}{3}\left(nhận\right)\end{matrix}\right.\)
\(\left(5x+1\right)^2=\dfrac{36}{49}\)
=>\(\left[{}\begin{matrix}5x+1=\dfrac{6}{7}\\5x+1=-\dfrac{6}{7}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}5x=\dfrac{6}{7}-1=-\dfrac{1}{7}\\5x=-\dfrac{6}{7}-1=-\dfrac{13}{7}\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-\dfrac{1}{7}:5=-\dfrac{1}{35}\\x=-\dfrac{13}{7}:5=-\dfrac{13}{35}\end{matrix}\right.\)
\(\left(8x\right)^{2x+1}=5^{2x+1}\)
=>8x=5
=>\(x=\dfrac{5}{8}\)
\(x-\left(\dfrac{2}{9}\right)^3=\left(\dfrac{2}{3}\right)^6\)
=>\(x-\dfrac{8}{729}=\dfrac{64}{729}\)
=>\(x=\dfrac{64}{729}+\dfrac{8}{729}=\dfrac{72}{729}=\dfrac{8}{81}\)
Sửa đề: \(\left(x-2,5\right)^2+\left(y-\dfrac{1}{10}\right)^2< =0\)
mà \(\left(x-2,5\right)^2+\left(y-\dfrac{1}{10}\right)^2>=0\forall x,y\)
nên \(\left\{{}\begin{matrix}x-2,5=0\\y-\dfrac{1}{10}=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2,5\\y=\dfrac{1}{10}\end{matrix}\right.\)
`(5x + 1)^2 = 36/49`
TH1:
`(5x + 1)^2 = (6/7)^2`
`=> 5x + 1 = 6/7`
`=> 5x = 6/7 - 1`
`=> 5x = -1/7`
`=> x = -1/7 : 5`
`=> x = -1/35`
TH2:
`(5x + 1)^2 = (-6/7)^2`
`=> 5x + 1 = -6/7`
`=> 5x = -6/7 - 1`
`=> 5x = -13/7`
`=> x = - 13/7 :5`
`=> x = -13/35`
Vậy `x = -1/35 ; x = -13/35`
`b)(x - 2/9)^3 = (2/3)^6
`=> (x - 2/9)^3 = (8/27)^3`
`=> x - 2/9 = 8/27`
`=> x = 8/27 + 2/9`
`=> x = 14/27`
Vậy `x = 14/27`
`c)(8x)^(2x + 1) = 5^(2x + 1)`
`=> 8x = 5`
`=> x = 5 : 8`
`=> x = 5/8`
Vậy `x = 5/8`
`d)(x - 2,5)^2 + (y - 1/10)^2 ≥0`
TH1:
`x - 2.5 = 0`
=> x = 0 + 2,5`
`=> x = 2,5 = 5/2`
TH2:
`y - 1/10 = 0`
`=> y = 0 + 1/10`
`=> y = 1/10`
Vậy `x = 5/2 ` ; `y = 1/10`