so sánh 3^12 và 5^8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(5^{200}=25^{100}\)
\(3^{300}=27^{100}\)
mà 25<27
nên \(5^{200}< 3^{300}\)

a)
\(\dfrac{6}{12}=\dfrac{6:6}{12:6}=\dfrac{1}{2}\)
\(\Rightarrow\dfrac{1}{2}=\dfrac{1\times2}{2\times2}=\dfrac{2}{4}\)
Mà \(\dfrac{2}{4}< \dfrac{3}{4}\)
Vậy \(\dfrac{6}{12}< \dfrac{3}{4}\).
b)
\(\dfrac{8}{10}=\dfrac{8:2}{10:2}=\dfrac{4}{5}\)
Mà \(\dfrac{2}{5}< \dfrac{4}{5}\)
Vậy \(\dfrac{2}{5}< \dfrac{8}{10}\).
c)
\(\dfrac{40}{35}=\dfrac{40:5}{35:5}=\dfrac{8}{7}\)
Mà \(\dfrac{8}{7}>\dfrac{6}{7}\)
Vậy \(\dfrac{40}{35}>\dfrac{6}{7}\).
d)
\(\dfrac{8}{16}=\dfrac{8:8}{16:8}=\dfrac{1}{2}\)
Mà \(\dfrac{1}{2}< \dfrac{5}{2}\)
Vậy \(\dfrac{8}{16}< \dfrac{5}{2}\).

a: \(\dfrac{-8}{31}=\dfrac{-8\cdot101}{31\cdot101}=\dfrac{-808}{3131}\)
\(\dfrac{-789}{3131}=\dfrac{-789}{3131}\)
b: Thiếu phân số thứ hai rồi bạn
c: \(\dfrac{1}{n}=\dfrac{n+1}{n\left(n+1\right)}\)
\(\dfrac{1}{n+1}=\dfrac{n}{n\left(n+1\right)}\)

a, \(4^{100}=\left(2^2\right)^{100}=2^{200}< 2^{202}\)
\(\Rightarrow\text{ }4^{100}< 2^{202}\)
b, \(3^0=1< 5^8\)
\(3^0< 5^8\)
c, \(\left(0,6\right)^0=1\)
\(\left(-0,9\right)^6=\left(0,9\right)^6\)
\(\Rightarrow\text{ }\left(0,6\right)^0< \left(-0,9\right)^6\)
d,
e, \(8^{12}=\left(2^3\right)^{12}=2^{36}=2^{16}\cdot2^{20}=2^{16}\cdot\left(2^4\right)^5=2^{16}\cdot16^5\)
\(12^8=\left(2^2\cdot3\right)^8=2^{16}\cdot3^8=2^{16}\cdot\left(3^2\right)^4=2^{16}\cdot9^4\)
Vì \(2^{16}\cdot16^5>2^{16}\cdot9^4\text{ }\Rightarrow\text{ }8^{12}>12^8\)

đúng boi vi theo t/c cua ty le thuc ta có;
a/b = c/d => ad=bc ( h trung ty = h ngoai ty)

\(5^9=\left(5^3\right)^3=125^3>81^3=\left(3^4\right)^3=3^{12}\)
Vậy \(5^9>3^{12}\)

Ta có: 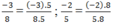
Vì (-3).5 > 8 . (-2) nên 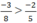
Với hai phân số 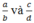 (a, b, c, d ∈ Z ; b > 0 ; d > 0) nếu
(a, b, c, d ∈ Z ; b > 0 ; d > 0) nếu 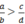 thì ad > bc hoặc
thì ad > bc hoặc 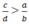 thì cb > ad
thì cb > ad
Ta chứng minh: 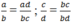
Ta có: 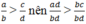
Theo quy tắc so sánh hai phân số ta có: ad > bc
Theo chiều ngược lại, ta cũng có:
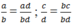
Theo quy tắc so sánh hai phân số nếu 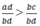
Suy ra 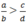

7/5 và 8/3
7/5 = 21/15
8/3 = 40/15
vậy 21/15 < 40/15 hay 7/5 < 8/3
\(3^{12}=3^{3.4}=\left(3^3\right)^4=27^4\)
\(5^8=5^{2.4}=\left(5^2\right)^4=25^4\)
Do \(27^4>25^4\) nên \(3^{12}>5^8\)