A=(x+2)2+\(|2y-3|\)+2024
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
0
1 tháng 11 2023
Sửa đề: \(5x^2+5y^2+8xy-2x+2y+2=0\)
=>\(4x^2+8xy+4y^2+x^2-2x+1+y^2+2y+1=0\)
=>\(\left(2x+2y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\)
=>\(\left\{{}\begin{matrix}2x+2y=0\\x-1=0\\y+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-1\end{matrix}\right.\)
\(M=\left(x-y\right)^{2023}-\left(x-2\right)^{2024}+\left(y+1\right)^{2023}\)
\(=\left(1+1\right)^{2023}-\left(1-2\right)^{2024}+\left(-1+1\right)^{2023}\)
\(=2^{2023}-1\)
8 tháng 10 2023
\(5x^2+5y^2+8xy-2x+2y+2=0\)
=>\(4x^2+8xy+4y^2+x^2-2x+1+y^2+2y+1=0\)
=>\(4\left(x+y\right)^2+\left(x-1\right)^2+\left(y+1\right)^2=0\)
=>x=1 và y=-1
\(M=\left(1-1\right)^{2023}+\left(1-2\right)^{2024}+\left(-1+1\right)^{2025}=1\)
KV
1 tháng 11 2023
(x + 20)⁴ + (2y - 1)²⁰²⁴ ≤ 0
⇒ (x + 20)⁴ = 0 và (2y - 1)²⁰²⁴ = 0
*) (x + 20)⁴ = 0
x + 20 = 0
x = 0 - 20
x = -20
*) (2y - 1)²⁰²⁴ = 0
2y - 1 = 0
2y = 1
y = 1/2
M = 5.(-20)².1/2 - 4.(-2).(1/2)²
= 1000 + 2
= 1002
TB
1
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
19 tháng 12
(y - 1)2024 + |\(x+y-1\)| = 0
Vì (y - 1)2024 ≥ 0 ∀ y; |\(x+y-1\)| ≥ 0 ∀ \(x;y\)
(y - 1)2024 + |\(x+y-1\)| = 0 khi và chỉ khi
y - 1 = 0 và \(x+y-1\) = 0
y - 1 = 0 Suy ra y = 1. thay y = 1 vào biểu thức \(x+y-1=0\) ta có:
\(x+1-1=0\) ⇒ \(x=0-1+1\) \(x=0\)
Vậy \(x=0;y=1\) thay vào biểu thức A= \(x^{2024}\) + y2024 ta được:
A = 02024 + 12024 = 0 + 1 = 1
17 tháng 11 2021
\(\Leftrightarrow x=2-\sqrt{3}\)
Dễ thấy x là nghiệm của PT \(x^2-4x+1\)
\(H=\left(x^5-4x^4+x^3\right)+\left(x^4-4x^3+x^2\right)+\left(5x^2-20x+5\right)+2019\\ H=\left(x^2-4x+1\right)\left(x^3+x^2+5\right)+2019\\ H=2019\)
LT
2
1 tháng 9 2015
a=[(2x)^2+2.2x.3+3^2]+(y^2-2y+1)+2014
=(2x+3)^2+(y-1)^2+2014
ta thấy
2x+3)^2>=0 voi moi x
(y-1)^2>=0 voi moi y
=>(2x+3)^2+(y-1)^2+2014>=2014
a>=2014 dấu = xay ra khi;
2x+3)^2=0 va (y-1)^2=0
=>x=-3/2:y=1
28 tháng 9 2018
\(4x^2+12x+y^2-2y+2024\)
\(=\left(4x^2+12x+9\right)+\left(y^2-2y+1\right)+2014\)
\(=\left(2x+3\right)^2+\left(y-1\right)^2+2014\)
Dấu "=" xảy ra <=> x = -3/2; y = 1
Vậy...
LT
1
28 tháng 9 2018
\(4x^2+12x+y^2-2y+2024\)
\(=\left(4x^2+12x+9\right)+\left(y^2-2y+1\right)+2014\)
\(=\left(2x+3\right)^2+\left(y-1\right)^2+2014\)
Dấu "=" xảy ra <=> x = -3/2; y = 1
Vậy...
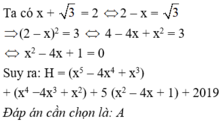
Ta có:
`(x+2)^2>=0` với mọi x
`|2y-3|>=0` với mọi y
`=>A=(x+2)^2+|2y-3|+2024>=2024` với mọi x,y
Dấu "=" xảy ra:
`x+2=0` và `2y-3=0`
`<=>x=-2` và `2y=3`
`<=>x=-2` và y=3/2`