tính a= 3+3 mũ 2+ 3 mũ 3+...+ 3 mũ 2015
tìm x : 2xA + 3= 3 mũ 4 x X
cần gấp ak, ai nhanh mk tik cho
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 10 2021
Bài 3:
#include <bits/stdc++.h>
using namespace std;
double a,b,c,delta,x1,x2;
int main()
{
//freopen("PTB2.inp","r",stdin);
//freopen("PTB2.out","w",stdout);
cin>>a>>b>>c;
delta=(b*b-4*a*c);
if (delta<0) cout<<"-1";
if (delta==0) cout<<fixed<<setprecision(5)<<(-b/(2*a));
if (delta>0)
{
x1=(-b-sqrt(delta))/(2*a);
x2=(-b+sqrt(delta))/(2*a);
cout<<fixed<<setprecision(5)<<x1<<" "<<fixed<<setprecision(5)<<x2;
}
return 0;
}
24 tháng 10 2021
4 bước : xác định bài toán , ý tưởng , thuật toán , mô phỏng làm như nào ạ ?
KV
10 tháng 5 2023
a) Phương trình bậc nhất một ẩn là phương trình có dạng ax + b = 0 (với a ≠ 0)
Ví dụ: 2x + 4 = 0
a = 2; b = 4
b) Công thức tính thể tích hình hộp chữ nhật:
V = Sh
Với V là thể tích, S là diện tích 1 đáy, h là chiều cao
c)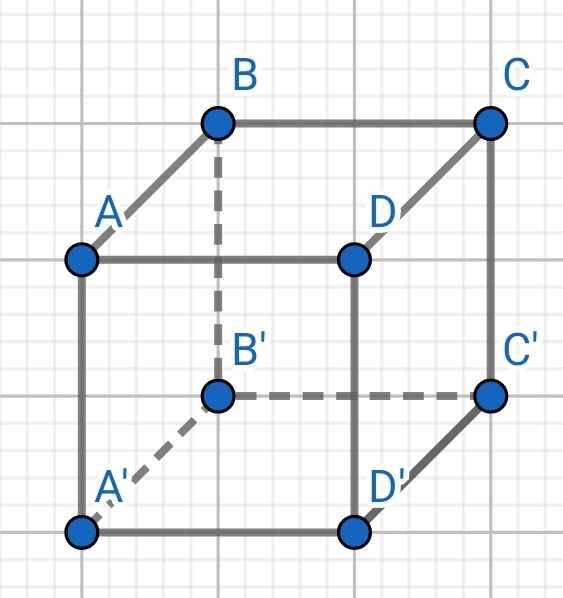 
Thể tích:
V = AB.AD.AA'
= 12 . 16 . 25 = 4800 (cm³)
10 tháng 5 2023
a: ax+b=0(a<>0) là phương trình bậc nhất một ẩn
b: V=a*b*c
a,b là chiều dài, chiều rộng
c là chiều cao
c: V=12*16*25=4800cm3
ML
17 tháng 4 2022
**Phần tử không phải phương trình bạn nha.
Bài làm:
Program HOC24;
var N,i: integer;
t: longint;
begin
write('Nhap so phan tu: '); readln(n);
for i:=1 to n do
begin
write('Nhap phan tu thu ',i,': '); readln(a[i]);
end;
t:=0;
for i:=1 to n do t:=t+a[i];
writeln('Tong day so la: ',t);
readln
end.
20 tháng 10 2021
a:
#include <bits/stdc++.h>
using namespace std;
long long n,x,i,t;
int main()
{
cin>>n;
t=0;
for (i=1; i<=n; i++)
{
cin>>x;
t=t+x;
}
cout<<t;
return 0;
}
T
0
TL
19 tháng 8 2023
Tham khảo:
a) Gợi ý:
Ý tưởng
Dùng một vòng do while để nhập a, b, c nếu a = 0, thì nhập lại.
Chúng ta dùng hàm sqrt() trong thư viện math.h để tính căn delta hoặc tính căn không dùng hàm sqrt()tại đây.
Chúng ta tạo hàm giaiPT trả về kiểu int chính là số nghiệm của phương trình (1).
Chúng ta sẽ đưa tham chiếu 2 biến x1 , x2 vào hàm giaiPT để gán giá trị hai nghiệm.
Nếu pt (1) vô nghiện thì giaiPT sẽ trả về 0 , đồng thời gán x1 = x2 =0 .
Nếu pt (1) có nghiệm kép thì giaiPT sẽ trả về 1 , đồng thời gán x1 = x2 = -b/2a .
Nếu pt (1) có 2 nghiệm thì giaiPT sẽ trả về 2 , gán x1 = (-b+√delta ) / 2a x = (-b-√delta ) / 2a .
b) Gợi ý:
#include <iostream>
using namespace std;
void nhap(int &n, int a[]){
for(int i=0;i<n;i++){
cout<<"a["<<i+1<<"]= ";cin>>a[i];
}
}
void xuat(int n, int a[]){
for(int i=0;i<n;i++){
cout<<a[i]<<" ";
}
}
int tinhTBCongint (int n, int a[]){
int sum=0, dem=0;
for(int i=0;i<n;i++){
sum+=a[i]; dem++;
}
return sum/n;
}
int tinhTBCongDuong(int n, int a[]){
int sum=0, dem=0;
for(int i=0;i<n;i++){
if(a[i] > 0) {
sum+=a[i]; dem++;
}
}
if(dem==0) return 0;
return sum/dem;
}
int tinhTBCongAm(int n, int a[]){
int sum=0, dem=0;
for(int i=0;i<n;i++){
if(a[i]<0) {
sum+=a[i]; dem++;
}
}
if(dem==0) return 0;
return sum/dem;
}
int main(){
int n;
int a[100];
do{
cout<<"Nhap n: "; cin>>n;
}while(n <= 0 || n >=100);
nhap(n,a);
cout<<"\n--------XUAT MANG----\n";
xuat(n,a);
cout<<"Trung binh cong: "<<tinhTBCongint(n,a)<<"\n\n";
cout<<"Trung binh so duong: "<<tinhTBCongDuong(n,a)<<"\n\n";
cout<<"Trung binh so am: "<<tinhTBCongAm(n,a)<<"\n\n";
}
TL
19 tháng 8 2023
Tham khảo:
a) Gợi ý:
Ý tưởng
Dùng một vòng do while để nhập a, b, c nếu a = 0, thì nhập lại.
Chúng ta dùng hàm sqrt() trong thư viện math.h để tính căn delta hoặc tính căn không dùng hàm sqrt()tại đây.
Chúng ta tạo hàm giaiPT trả về kiểu int chính là số nghiệm của phương trình (1).
Chúng ta sẽ đưa tham chiếu 2 biến x1 , x2 vào hàm giaiPT để gán giá trị hai nghiệm.
Nếu pt (1) vô nghiện thì giaiPT sẽ trả về 0 , đồng thời gán x1 = x2 =0 .
Nếu pt (1) có nghiệm kép thì giaiPT sẽ trả về 1 , đồng thời gán x1 = x2 = -b/2a .
Nếu pt (1) có 2 nghiệm thì giaiPT sẽ trả về 2 , gán x1 = (-b+√delta ) / 2a x = (-b-√delta ) / 2a .
b) Gợi ý:
#include <iostream>
using namespace std;
void nhap(int &n, int a[]){
for(int i=0;i<n;i++){
cout<<"a["<<i+1<<"]= ";cin>>a[i];
}
}
void xuat(int n, int a[]){
for(int i=0;i<n;i++){
cout<<a[i]<<" ";
}
}
int tinhTBCongint (int n, int a[]){
int sum=0, dem=0;
for(int i=0;i<n;i++){
sum+=a[i]; dem++;
}
return sum/n;
}
int tinhTBCongDuong(int n, int a[]){
int sum=0, dem=0;
for(int i=0;i<n;i++){
if(a[i] > 0) {
sum+=a[i]; dem++;
}
}
if(dem==0) return 0;
return sum/dem;
}
int tinhTBCongAm(int n, int a[]){
int sum=0, dem=0;
for(int i=0;i<n;i++){
if(a[i]<0) {
sum+=a[i]; dem++;
}
}
if(dem==0) return 0;
return sum/dem;
}
int main(){
int n;
int a[100];
do{
cout<<"Nhap n: "; cin>>n;
}while(n <= 0 || n >=100);
nhap(n,a);
cout<<"\n--------XUAT MANG----\n";
xuat(n,a);
cout<<"Trung binh cong: "<<tinhTBCongint(n,a)<<"\n\n";
cout<<"Trung binh so duong: "<<tinhTBCongDuong(n,a)<<"\n\n";
cout<<"Trung binh so am: "<<tinhTBCongAm(n,a)<<"\n\n";
}
HQ
Hà Quang Minh
Giáo viên
13 tháng 9 2023
a) Phương trình \(7x + \dfrac{4}{7} = 0\) là phương trình bậc nhất một ẩn vì có dạng \(ax + b = 0\) với \(a\) và \(b\) là các hệ số đã cho và \(a \ne 0\), \(x\) là ẩn số.
Khi đó, \(a = 7;b = \dfrac{4}{7}\).
b) \(\dfrac{3}{2}y - 5 = 4\)
\(\dfrac{3}{2}y - 5 - 4 = 0\)
\(\dfrac{3}{2}y - 9 = 0\)
Phương trình \(\dfrac{3}{2}y - 9 = 0\) là phương trình bậc nhất một ẩn vì có dạng \(ay + b = 0\) với \(a\) và \(b\) là các hệ số đã cho và \(a \ne 0\), \(y\) là ẩn số.
Khi đó, \(a = \dfrac{3}{2};b = - 9\)
c) Phương trình \(0t + 6 = 0\) không là phương trình bậc nhất một ẩn.
Mặc dù phương trình đã cho có dạng \(at + b = 0\) với \(a\) và \(b\) là các hệ số đã cho nhưng \(a = 0\).
d) Phương trình \({x^2} + 3 = 0\) không là phương trình bậc nhất một ẩn vì không có dạng \(ax + b = 0\) với \(a\) và \(b\) là các hệ số đã cho và \(a \ne 0\), \(x\) là ẩn số (do có \({x^2}\)).
7 tháng 3 2022
1: Hai phương trình gọi là tương đương khi chúng có chung tập nghiệm
2: Phương trình bậc nhất một ẩn là phương trình có dạng ax+b=0(a<>0), với a,b là các số thực
PN
1
Y
4 tháng 1 2022
Tham khảo:
Thuật toán giải phương trình ax + b = 0
- Bằng liệt kê tuần tự
Bước 1: Nhập hai số thực a, b
Bước 2. Nếu a = 0
Bước 2.1. Nếu b ≠0 thì thông báo phương trình vô định, rồi kết thúc;
Bước 2.2. Nếu b = 0 thì gán x <- 0 rồi chuyển sang bước 4;
Bước 3: x <- -b/a
Bước 4. Đưa ra nghiệm X, rồi kết thúc.
- Sơ đồ khối:
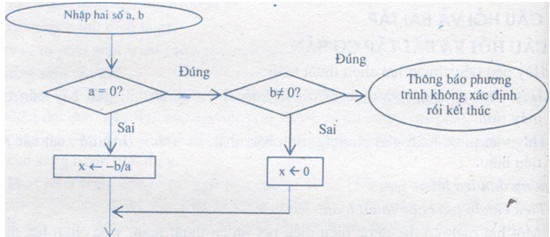
Đề xuất các test tiêu chuẩn
Để xét tất cả các trường hợp có thể xảy ra, ta sử dụng ba bộ test như sau:
i) a = 0, b = 1 (kiểm tra trường hợp phương trình vô định);
ii) a = 0,b = 0 (kiểm tra trường hợp nghiệm x=0);
iii) a = 3, b = 6 (kiểm tra trường hợp nghiêm , y = -b/a)
A = 3 + 32 + 33 + ... + 32015
3A = 32 + 33 + 34 + ... + 32016
3A - A = 32 + 33 + 34 + ... + 32016
2A = 32 + 33 + 34 + ... + 32016 - (3 + 32 + 33 + ... + 32015)
2A = 32 + 33 + 34 + ... + 32016 - 3 - 32 - 33 - ... - 32015
2 A = 3 2016 - 3 + (32 - 32) + (33 - 33) + ... + (32015 - 32015)
2A = 32016 - 3 + 0 + 0 + ... + 0 + 0
2A = 32016 - 3
2A + 3 = 32016 - 3 + 3
2A + 3 = 32016 - (3 - 3) = 34\(x\)
32016 = 34\(x\)
2016 = 4\(x\)
\(x\) = 2016 : 4
\(x=\) 504
Vậy \(x=504\)