f(x) = ax^2 + bx + c, f(2) = 0, CMR f(x) chia hết cho x - 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 6 2019
Đáp án D
Ta có f ' x = - e x . f 2 x ⇔ - f ' x f 2 x = e x ⇔ ∫ - f ' x f 2 x d x = ∫ e x d x ⇔ 1 f x = e x + C
Mà f 0 = 1 2 ⇒ 1 f 0 = e 0 + C ⇔ C + 1 = 2 ⇒ C = 1 → f x = 1 e x + 1
Do đó f ' x = - e x e x + 1 2 ⇒ f ' ln 2 = - 2 9 . Vậy phương trình tiếp tuyến là 2 x + 9 y - 2 ln 2 - 3 = 0 .
CM
12 tháng 9 2017
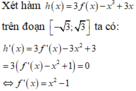
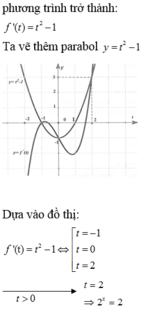
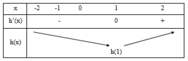
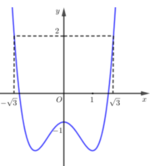
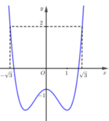
Dựng đồ thị hàm số y = x 2 - 1 cùng một hệ trục tọa độ với đồ thị hàm số y=f’(x) bài cho ta được:
.
.
.
.
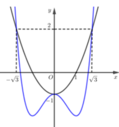
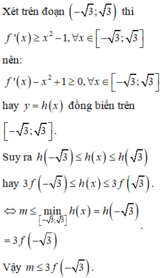
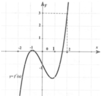
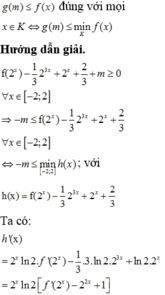
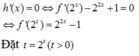
f(2)=0
=>\(a\cdot2^2+b\cdot2+c=0\)
=>4a+2b+c=0
=>c=-4a-2b
=>\(f\left(x\right)=ax^2+bx-4a-2b\)
\(=a\left(x^2-4\right)+b\left(x-2\right)\)
\(=a\left(x-2\right)\left(x+2\right)+b\left(x-2\right)\)
\(=\left(x-2\right)\left(ax+2a+b\right)⋮x-2\)