Cho tam giác ABC vuông tại A có AB là 6 cm AC là 8 cm Lấy d là điểm chính giữa cạnh AB trên cạnh ac lấy điểm E sao cho AE gấp 3 lần CE
A)tính S tam giác
B) tính số phần trăm diện tích tứ giác bce và diện tích tam giác ABC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

 Tổng số phần của 2 diện tích tam giác :
Tổng số phần của 2 diện tích tam giác :
3 + 2 =5 ( phần )
Diện tích tam giác ACD :
70 : 5 x 3 = 52 ( cm2)
Diện tích tam giác ABC :
70 : 5 x 2 = 28 ( cm2)
Vậy : diện tích tam giác ACD : 52 cm2
______________ ABC : 28 cm2

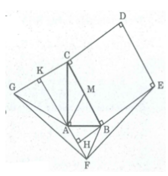
A G K C D E B H F M a
a) Giả sử M là trung điểm của BC, \(\Delta ABM\) là tam giác đều nên \(\widehat{ABC}=60^o.\)
Từ đó suy ra: \(\widehat{BCA}=30^o\). Theo định lí Py-ta-go, ta có:
AC = \(\sqrt{BC^2-AB^2}\)
AC = \(\sqrt{4a^2-a^2}=a\sqrt{3}.\)
Do đó, ta có:
SABC = \(\dfrac{1}{2}AB.AC=\dfrac{1}{2}a^2\sqrt{3}.\) (1)
b) Vì \(\widehat{FAB}=\widehat{ABC}=60^o\) nên FA // BC (hai góc so le trong), từ đó suy ra FA vuông góc với BE và CG.
Gọi giao điểm của FA và BE là H, giao điểm của FA và CG là K. Ta có:
SFAG = \(\dfrac{1}{2}FA.GK=\dfrac{1}{2}a.\dfrac{a\sqrt{3}}{2}=\dfrac{1}{4}a^2\sqrt{3},\) (2)
SFBE = \(\dfrac{1}{2}BE.FH=\dfrac{1}{2}.2a.\dfrac{a}{2}=\dfrac{1}{2}a^2.\) (3)
c) SBDCE = 4a2, (4)
SABF = \(\dfrac{1}{4}a^2\sqrt{3},\) (5)
SACG = \(\dfrac{3}{4}a^2\sqrt{3}.\) (6)
Từ (1), (2), (3), (4), (5), (6), ta có:
SDEFG = \(\dfrac{a^2}{4}\left(18+7\sqrt{3}\right)\approx7,53a^2.\)

S B C D E = B C 2 = 2 a 2 = 4 a 2 (dvdt)
Trong tam giác vuông BHA, theo Pi-ta-go, ta có: A H 2 + B H 2 = A B 2
⇒ B H 2 = A B 2 - A H 2 = a 2 - a 2 / 4 = 3 a 2 / 4 ⇒ BH = (a 3 )/2
S
A
B
F
= 1/2 BH.FA = 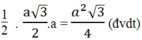
Trong tam giác vuông AKG, theo Pi-ta-go, ta có: A C 2 = A K 2 + K C 2
⇒ A K 2 = A C 2 - K C 2 = 3 a 2 - 3 a 2 / 4 = 9 a 2 / 4 ⇒ AK = 3a/2 (đvdt)
S
A
C
G
= 1/2 AK.CG = 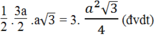
S D E F G = S B C D E + S F B E + S FAB + S F A G + S A C G + S A B C
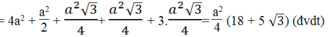
Giúp mình 😭
a: ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot6\cdot8=24\left(cm^2\right)\)
b: AE=3CE
mà AE+CE=AC
nên \(CE=\dfrac{1}{4}AC\)
=>\(\dfrac{S_{CBE}}{S_{CAB}}=\dfrac{CE}{CA}=\dfrac{1}{4}=25\%\)