cho tam giác ABC vuông tại A, M là trung điểm của AB. Trên tia đối của tia MC lấy điểm N sao cho MN = MC. Chứng Minh: a) AN = BC b) BN vuông góc với AB c) AC // BN
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 3 2022
a: Xét ΔABN vuông tại N và ΔACM vuông tại M có
AB=AC
\(\widehat{BAN}\) chung
Do đó: ΔABN=ΔACM
Suy ra: BN=CM
b: Xét ΔMBC vuông tại M và ΔNCB vuông tại N có
BC chung
MC=BN
Do đó: ΔMBC=ΔNCB
Suy ra: \(\widehat{HCB}=\widehat{HBC}\)
hay ΔHBC cân tại H
c: Xét ΔABC có AM/AB=AN/AC
nên MN//BC
10 tháng 8 2021
a: Xét \(\left(O\right)\) có
\(\widehat{CNB}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{CNB}=90^0\)
hay CM\(\perp\)AB
Xét \(\left(O\right)\) có
\(\widehat{BNC}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{BNC}=90^0\)
hay BN\(\perp\)AC
b: Xét ΔABC có
BN là đường cao ứng với cạnh AC
CM là đường cao ứng với cạnh AB
BN cắt CM tại H
Do đó: AH\(\perp\)BC
TH
4 tháng 3 2020
a, xét ΔAMC và ΔANB có : ^A chung
AB = AC do ΔABC cân tại A (gt)
^ANB = ^AMC = 90
=> ΔAMC = ΔANB (ch-gn)
=> AM = AN (định nghĩa)
b, xét ΔBMC và ΔCNB có : BC chung
^ABC = ^ACB do ΔABC cân tại A (gt)
^BMC = ^CNB = 90
=> ΔBMC = ΔCAB (ch-gn)
=> ^HBC = ^HCB (định nghĩa)
=> ΔHBC cân tại H (định nghĩa)
=> HB = HC
=> H thuộc đường trung trực của BC (định lí)
AB = AC (Câu a) => A thuộc đường trung trực của BC (Định lí)
=> AH là trung trực của CB (đl)
4 tháng 3 2020
Bài làm
a) Xét tam giác AMC và tam giác ANB có:
^AMC = ^ANB = 90°
Cạnh huyền: AB = AC ( tam giác ABC cân )
Góc nhọn: ^A chung.
=> ∆AMC = ∆ANB ( cạnh huyền-góc nhọn )
=> AM = AN ( hai cạnh tương ứng )
b) Xét tam giác ABC có:
CM | AB ( gt )
BN | AC
Mà CM cắt BN tại H
=> H là trực tâm.
=> AH | BC
Mà tam giác ABC cân tại A
=> AH vừa là đường cao vừa là đường trung tuyến.
=> AH là trung trực của BC . ( Đpcm )
c) Gọi giao điểm của AH và BC là I
Nối NI, và NI // MB ( bạn có thể tìm cách chứng minh nó song song ), nối MN
Vì AM = AN => Tam giác AMN cân tại A
=> ^AMN = ( 180° - ^A )/2
Tam giác ABC cân tại A => ^ABC = ( 180° - ^A )/2
=> ^AMN = ^ ABC mà 2 góc này ở vị trí đồng vị.
=> MN // BC.
=> ^MNB = ^NBI
Xét tam giác BMN và tam giác NIB có:
^MNB = ^NBI ( so le trong)
BN chung.
^MBN = ^INB ( so le trong )
=> ∆BMN = ∆NIB ( g.c.g )
=> MN = IB
Mà BI = IC ( do AI trung trực )
=> IC = MN
=> ( BI + IC )/2 = MN
=> 2MN = BC ( đpcm )
12 tháng 2 2022
a. xét tam giác ABH và tam giác ACH
AB = AC ( ABC cân )
góc B = góc C ( ABC cân )
BH = CH ( ABC cân, AH là đường cao cũng là trung tuyến )
Vậy tam giác ABH = tam giác ACH ( c.g.c )
b. xét tam giác vuông BNH và tam giác vuông CNH
BN = CM ( AB = AC ; AM = AN )
BH = CH
Vậy tam giác vuông BNH = tam giác vuông CNH ( cạnh huyền. cạnh góc vuông )
c. áp dụng định lý pitao vào tam giác vuông AHB:
\(AB^2=AH^2+BH^2\)
\(BH=\sqrt{10^2-8^2}=\sqrt{64}=8cm\)
=> BC = BH. 2 = 8.2 =16 cm
Chúc bạn học tốt!!!
12 tháng 2 2022
a, Xét tam giác ABH và tam giác ACH
^AHB = ^AHC = 900
AB = AC (gt)
AH _ chung
Vậy tam giác ABH = tam giác ACH ( ch - cgv )
b, Xét tam ANB và tam giác AMC có :
^A _ chung
AM = AN(gt)
AB = AC (gt)
Vậy tam giác ANB = tam giác AMC ( c.g.c )
=> BN = CM ( 2 cạnh tương ứng )
c, Xét tam giác ABH vuông tại H, theo định lí Pytago
\(BH=\sqrt{AB^2-AH^2}=6cm\)
Xét tam giác ABC cân tại A có AH là đường cao nên đồng thời AH là đường trung tuyến
=> BC = 2BH = 12 cm
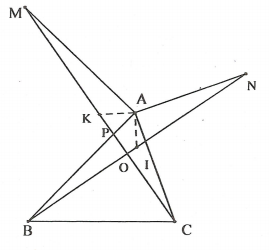
a: Xét ΔMAN và ΔMBC có
MA=MB
\(\widehat{AMN}=\widehat{BMC}\)(hai góc đối đỉnh)
MN=MC
Do đó: ΔMAN=ΔMBC
=>AN=BC
b: Xét ΔMBN và ΔMAC có
MB=MA
\(\widehat{BMN}=\widehat{AMC}\)(hai góc đối đỉnh)
MN=MC
Do đó: ΔMBN=ΔMAC
=>\(\widehat{MBN}=\widehat{MAC}\)
mà hai góc này là hai góc ở vị trí so le trong nên BN//AC
c: BN//AC
AB\(\perp\)AC
Do đó: BN\(\perp\)AB