cho hình 3.59 biết abc + cde = bcd + 180 độ hãy chứng tỏ abF là góc vuông
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DH
Cho hình sau. Biết BF vuông góc EF, góc ABC
+ góc CDE = góc BCD = 180 độ. Chứng minh AB vuông góc BF
+ góc CDE = góc BCD = 180 độ. Chứng minh AB vuông góc BF
0
LH
1
22 tháng 7 2023
góc BAD+góc BCD=180 độ
=>ABCD nội tiếp
=>góc ABD=góc ACD và góc CBD=góc CAD
mà góc ACD=góc CAD
nên góc ABD=góc CBD
=>BD là phân giác của góc ABC
19 tháng 9 2018
Hình nào?
không có hình thì làm làm sao được?
Bạn vẽ hình đi :)
CM
25 tháng 3 2018
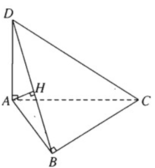
Vì AD ⊥ (ABC) nên AD ⊥ BC
Ngoài ra BC ⊥ AB nên ta có BC ⊥ (ABD)
Vì mặt phẳng (BCD) chứa BC mà BC ⊥ (ABD) nên ta suy ra mặt phẳng (BCD) vuông góc với mặt phẳng (ABD).
Hai mặt phẳng (BCD) và (ABD) vuông góc với nhau và có giao tuyến là BD. Đường thẳng AH thuộc mặt phẳng (ABD) và vuông góc với giao tuyến BD nên AH vuông góc với mặt phẳng (BCD).
26 tháng 2 2021
a) Xét ΔAFC vuông tại F có \(\widehat{A}=45^0\)(gt)
nên ΔAFC vuông cân tại F(Dấu hiệu nhận biết tam giác vuông cân)
hay FA=FC(hai cạnh bên)(đpcm)
5 tháng 2 2022
a: Xét tứ giác BHCD có
BH//CD
BD//CH
DO đó: BHCD là hình bình hành
b: Xét tứ giác ABDC có \(\widehat{ABD}+\widehat{ACD}=180^0\)
nên ABDC là tứ giác nội tiếp
Suy ra: \(\widehat{BAC}+\widehat{BDC}=180^0\)
c: Ta có: BHCD là hình bình hành
nên hai đường chéo BC và HD cắt nhau tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HD
hay H,M,D thẳng hàng
Hình đâu rồi bạn?