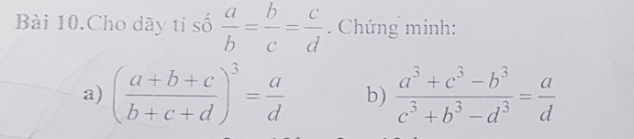 giúp e với ạ, e cảm ơn
giúp e với ạ, e cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


BÀI TOÁN DÂN SỐ
(Thái An)
I. KIẾN THỨC CƠ BẢN
1. Về vấn đề nêu trong văn bản:
Viết về hiểm hoạ của việc gia tăng dân số quá nhanh - một đề tài vừa khó vừa khô khan, tác giả đã chọn cách vào đề thật hấp dẫn, vừa thực tế, vừa giàu sức thuyết phục. Từ câu chuyện nhà giàu kén rể đến 64 ô bàn cờ với một lượng tóc "nhiều đến mức có thể phủ khắp bề mặt Trái Đất", bạn đọc dễ dàng hình dung về sự gia tăng dân số chóng mặt với tốc độ sinh sản như hiện nay.
2. Về cấu trúc và giá trị nội dung của văn bản:
a) Đề cập về một vấn đề bức xúc trong đời sống xã hội, văn bản Bài toán dân số được cấu trúc thành ba phần: Phần mở bài (từ đầu cho đến "sáng mắt ra"...), tác giả nêu ra vấn đề: bài toán dân số và kế hoạch hoá gia đình đã được đặt ra từ thời cổ đại; Phần thân bài (từ "Đó là câu chuyện từ bài toán cổ..." cho đến "...sang ô thứ 31 của bàn cờ"), tác giả làm rõ vấn đề đã được nêu ra: Tốc độ gia tăng nhanh chóng của dân số thế giới và Phần kết bài (từ "Đừng để cho..." đến hết): kêu gọi loài người cần kiềm chế tốc độ gia tăng dân số.
b) Trước hết, bài toán cổ và ý nghĩa về sự gia tăng nhanh chóng của số lượng: ô đầu tiên của bàn cờ chỉ là một hạt thóc, nếu gia tăng theo cấp số nhân thì đến hết 64 ô. Tốc độ gia tăng thực sự rất lớn ngoài sức tưởng tượng.
Thứ hai, sự gia tăng dân số của thế giới giống như lượng thóc tăng lên trong các ô bàn cờ. Lịch sử loài người tính đến năm 1995 đã là 5,63 tỉ người, nằm ở khoảng ô thứ ba mươi của bàn cờ trong bài toán cổ.
Thứ ba, để mỗi gia đình chỉ sinh hai con là điều rất khó thực hiện, vì trên thực tế, tỉ lệ phổ biến là phụ nữ sinh hơn hai con. Trong khi nếu đúng là mỗi gia đình chỉ sinh hai con thì chúng ta đang "mon men sang ô thứ 31 của bàn cờ".
c) Về cách thức thể hiện, với việc sử dụng câu chuyện kén rể của nhà thông thái, tác giả đã làm nổi bật vấn đề tốc độ gia tăng dân số; đồng thời làm tăng sức hấp dẫn cho bài viết. Mượn xưa để nói nay, sự giống nhau giữa số thóc tăng theo cấp số nhân với công bội hai và tình trạng bùng nổ dân số cả khi mỗi gia đình chỉ sinh hai con đã cho người đọc hình dung được một cách cụ thể về tốc độ gia tăng dân số. Tốc độ gia tăng nhanh đến mức bùng nổ được cảnh báo bằng hình ảnh một lượng thóc khổng lồ "có thể phủ kín bề mặt Trái Đất"...
c) Vì chính cuộc sống của chúng ta, hãy nhận thức đầy đủ về vấn đề dân số, cùng có trách nhiệm trong việc hạn chế sự gia tăng dân số. Đây chính là điều mà tác giả của bài viết mong muốn ở người đọc.
II. RÈN LUYỆN KĨ NĂNG
Văn bản ngắn gọn, trong đó các con số nói lên được nhiều điều. Cần đọc to, rõ ràng các con số để làm tăng thêm sức thuyết phục cho các lập luận của tác giả.
Soạn bài: Bài toán dân số
Hướng dẫn soạn bài
Tóm tắt :
Bài toán dân số là một vấn đề không mới. Tác giả nêu câu chuyện kén rể của nhà thông thái từ một bài toán cổ trên 1 bàn cờ tướng 64 ô. Theo đó thì thừ khai thiên lập địa đến năm 1995, dân số thế giới đạt đến ô thứ 30 với điều kiện mỗi gia đình chỉ có 2 con. Trong thực tế 1 phụ nữ có thể sinh nhiều con. Tính theo bài toán cổ thì số dân đã mon men sang ô thứ 34 của bàn cờ. Cuối cùng tác giả báo động về con đường “tồn tại hay không tồn tại”.
Bố cục :
- Phần 1 (từ đầu … sáng mắt ra) : Bài toán dân số đặt ra từ thời cổ đại.
- Phần 2 (tiếp … ô thứ 31 của bàn cờ) : Sự tăng nhanh khủng khiếp của dân số.
+ Luận điểm 1 (Đó là câu… nhường nào) : Câu chuyện kén rể của nhà thông thái.
+ Luận điểm 2 (bây giờ … không quá 5%) : Sự phát triển của dân số thế giới.
+ Luận điểm 3 (trong thực tế … 34 của bàn cờ): tỉ lệ sinh của phụ nữ Á và Phi.
- Phần 3 (còn lại) : kêu gọi loài người hạn chế gia tăng dân số.
Câu 1 (trang 131 sgk Ngữ Văn 8 Tập 1): (bố cục như đã chia phần trên)
Câu 2 (trang 131 sgk Ngữ Văn 8 Tập 1):
- Vấn đề chính tác giả muốn đặt ra : sự gia tăng dân số thế giới tốc độ chóng mặt, con người cần hạn chế sự gia tăng dân số để tồn tại.
- Điều làm tác giả sáng mắt ra là sự gia tăng dân số trong thời buổi nay đã được đặt trong một bài toán cổ đại.
Câu 3 (trang 131 sgk Ngữ Văn 8 Tập 1):
Câu chuyện kén rể của nhà thông thái làm nổi bật vấn đề gia tăng dân số, sự liên tưởng đến số thóc với dân số thật bất ngờ, thú vị, tạo nên hình dung cụ thể.
Câu 4 (trang 132 sgk Ngữ Văn 8 Tập 1):
- Việc đưa ra những con số về tỉ lệ sinh con là bằng chứng rõ ràng cho thấy tỉ lệ sinh của phụ nữ Á, Phi vô cùng mạnh.
- Các nước thuộc châu Phi có Nê-pan, Ru-an-đa, Tan-za-ni-a, Ma-đa-gát-xca. Các nước Việt Nam, Ấn Độ thuộc châu Á. Hai châu lục này có tỉ lệ các nước kém phát triển cao, nghèo, và tỉ lệ gia tăng dân số mạnh.
Câu 5 (trang 132 sgk Ngữ Văn 8 Tập 1):
Văn bản này đưa đến cho chúng ta hiểu biết về tình hình gia tăng dân số đáng báo động trên thế giới và Việt Nam, để từ đó chúng ta có hành động thiết thực.
Luyện tập
Câu 1 (trang 132 sgk Ngữ Văn 8 Tập 1):
Con đường tốt nhất để hạn chế sự gia tăng dân số là đẩy mạnh giáo dục, đặc biệt là giáo dục phụ nữ.
Câu 2 (trang 132 sgk Ngữ Văn 8 Tập 1):
Sự gia tăng dân số có tầm quan trọng to lớn với tương lai nhân loại, nhất là với các dân tộc còn nghèo nàn, lạc hậu vì :
- Dân số tăng kèm theo nhu cầu kinh tế để nuôi dạy con cái.
- Gia đình đông con dễ dẫn đến sự giáo dục, chăm sóc thiếu chu đáo, thất học.
- Đất chật người đông, đời sống con người càng thêm khó khăn.
Câu 3 (trang 132 sgk Ngữ Văn 8 Tập 1):
Dân số tăng mỗi năm (từ năm 2000 đến 2010) là 77 258 877. Vậy từ năm 2000 – 2003, sau 3 năm dân số sẽ tăng 77 258 877 x 3 = 231 776 631.
Dân số Việt Nam theo số liệu thống kê vào năm 2016 là 94 104 871 người
⇒ gấp gần 2,5 lần so với Việt Nam.

Ta có: AB//CD(vì ABCD là hình thang)
=>góc ABD=góc CDB
Xét tam giác ABD và tam giác CDB:
AB=DC(GT)
Góc ABD=Góc CDB(cmt)
DB là cạnh chung
Vậy tam giác ABD=tam giác CDB(c.g.c)
=>AD=BC(2 cạnh tương ứng); góc ADB=góc CBD( 2 góc tương ứng)
Ta có: góc ABD=góc CBD(cmt)
Mà 2 góc này nằm ở vị trí so le trong nên AD//BC(theo tiên đề Ơ-clit)(đpcm)

Viết các phân số dưới dạng tối giản:
0,3=310;−56;−123=−53;413;0;0,3=310;−56;−123=−53;413;0;−0,875=−8751000=−78−0,875=−8751000=−78
- So sánh các số hữu tỉ dương với nhau:
Ta có : 310=39130;413=40130310=39130;413=40130
Vì 39<40


a,
\(C=\dfrac{1}{11}+\dfrac{1}{12}+\dfrac{1}{13}+...+\dfrac{1}{19}\\ C>0+0+0+...+0=0\left(1\right)\)
\(C=\dfrac{1}{11}+\dfrac{1}{12}+\dfrac{1}{13}+...+\dfrac{1}{19}\)
Ta có:
\(\dfrac{1}{11}< \dfrac{1}{10}\\ \dfrac{1}{12}< \dfrac{1}{10}\\ \dfrac{1}{13}< \dfrac{1}{10}\\ ...\\ \dfrac{1}{19}< \dfrac{1}{10}\)
\(\Rightarrow C< \dfrac{1}{10}+\dfrac{1}{10}+\dfrac{1}{10}+...+\dfrac{1}{10}\left(9\text{ phân số }\dfrac{1}{10}\right)\\ C< 9\cdot\dfrac{1}{10}\\ C< \dfrac{9}{10}< 1\left(2\right)\)
Từ (1) và (2) ta có:
\(0< C< 1\)
Rõ ràng \(0\) và \(1\) là hai số nguyên liên tiếp nên \(C\) không phải là số nguyên
Vậy \(C\) không phải là số nguyên (đpcm)
b,
\(D=2\left[\dfrac{1}{3}+\dfrac{1}{15}+\dfrac{1}{35}+...+\dfrac{1}{n\left(n+2\right)}\right]\\ D=\dfrac{2}{3}+\dfrac{2}{15}+\dfrac{2}{35}+...+\dfrac{2}{n\left(n+2\right)}\\ D>0+0+0+...+0=0\left(1\right)\)
Ta có:
\(D=\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+\dfrac{2}{5\cdot7}+...+\dfrac{2}{n\cdot\left(n+2\right)}\\ D=\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{n}-\dfrac{1}{n+2}\\ D=\dfrac{1}{1}-\dfrac{1}{n+2}\\ D=1-\dfrac{1}{n+2}< 1\left(\text{Vì }n>0\right)\left(2\right)\)
Từ (1) và (2) ta có:
\(0< D< 1\)
Rõ ràng \(0\) và \(1\) là hai số nguyên liên tiếp nên \(D\) không phải là số nguyên
Vậy \(D\) không phải là số nguyên (đpcm)
c,
\(E=\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{2}{7}+\dfrac{2}{9}+\dfrac{2}{11}\\ E=\dfrac{2}{6}+\dfrac{2}{8}+\dfrac{2}{10}+\dfrac{2}{7}+\dfrac{2}{9}+\dfrac{2}{11}\\ E=\dfrac{2}{6}+\dfrac{2}{7}+\dfrac{2}{8}+\dfrac{2}{9}+\dfrac{2}{10}+\dfrac{2}{11}\)
Ta có:
\(\dfrac{2}{6}>\dfrac{2}{12}\\ \dfrac{2}{7}>\dfrac{2}{12}\\ \dfrac{2}{8}>\dfrac{2}{12}\\ ...\\ \dfrac{2}{11}>\dfrac{2}{12}\)
\(\Rightarrow E>\dfrac{2}{12}+\dfrac{2}{12}+\dfrac{2}{12}+\dfrac{2}{12}+\dfrac{2}{12}+\dfrac{2}{12}\\ E>6\cdot\dfrac{2}{12}\\ E>\dfrac{12}{12}=1\left(1\right)\)
Mặt khác ta có:
\(\dfrac{2}{6}>\dfrac{2}{7}\\ \dfrac{2}{6}>\dfrac{2}{8}\\ \dfrac{2}{6}>\dfrac{2}{9}\\ ...\\ \dfrac{2}{6}>\dfrac{2}{11}\)
\(\Rightarrow E< \dfrac{2}{6}+\dfrac{2}{6}+\dfrac{2}{6}+\dfrac{2}{6}+\dfrac{2}{6}+\dfrac{2}{6}\\ E< 6\cdot\dfrac{2}{6}\\ E< 2\left(2\right)\)
Từ (1) và (2) ta có:
\(1< E< 2\)
Rõ ràng \(1\) và \(2\) là hai số nguyên liên tiếp nên \(E\) không phải là số nguyên
Vậy \(E\) không phải là số nguyên (đpcm)
c) \(E=\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{2}{7}+\dfrac{2}{9}+\dfrac{2}{11}\)
\(=\dfrac{2}{6}+\dfrac{2}{8}+\dfrac{2}{10}+\dfrac{2}{7}+\dfrac{2}{9}+\dfrac{2}{11}\)
\(=2\left(\dfrac{1}{6}+\dfrac{1}{7}+\dfrac{1}{8}+\dfrac{1}{9}+\dfrac{1}{10}+\dfrac{1}{11}\right)\)
Ta có: \(\dfrac{1}{6}>\dfrac{1}{7}>\dfrac{1}{8}>\dfrac{1}{9}>\dfrac{1}{10}>\dfrac{1}{11}\)
\(\Rightarrow E>2\left(\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}+\dfrac{1}{11}\right)=2\left(\dfrac{1}{11}.6\right)=2\cdot\dfrac{6}{11}=\dfrac{12}{11}>1\) (1)
\(E< 2\left(\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}+\dfrac{1}{6}\right)=2\left(\dfrac{1}{6}.6\right)=2.1=2\) (2)
Từ (1) và (2) suy ra 1 < E < 2 suy ra E không phải là số nguyên

gọi số đó là abcd
Ta thấy:
a có 4 cách chọn
b có 3 cách chọn(vì a đã chọn 1 chữ số )
c có 2 cách chọn
d có 1 cách chọn
Vậy có tất cả 1x2x3x4=24 cách chọn số
Đ/s:24 cách chọn

Bài 2:
Với x,y,z,t là số tự nhiên khác 0
Có \(\dfrac{x}{x+y+z+t}< \dfrac{x}{x+y+z}< \dfrac{x}{x+y}\)
\(\dfrac{y}{x+y+z+t}< \dfrac{y}{x+y+t}< \dfrac{y}{x+y}\)
\(\dfrac{z}{x+y+z+t}< \dfrac{z}{y+z+t}< \dfrac{z}{z+t}\)
\(\dfrac{t}{x+y+z+t}< \dfrac{t}{x+z+t}< \dfrac{t}{z+t}\)
Cộng vế với vế \(\Rightarrow1< M< \dfrac{x+y}{x+y}+\dfrac{z+t}{z+t}=2\)
=> M không là số tự nhiên.
Bài 1:
Ta có:
\(B=\dfrac{2008}{1}+\dfrac{2007}{2}+\dfrac{2006}{3}+...+\dfrac{2}{2007}+\dfrac{1}{2008}\)
\(B=\left(1+\dfrac{2007}{2}\right)+\left(1+\dfrac{2006}{3}\right)+...+\left(1+\dfrac{2}{2007}\right)+\left(1+\dfrac{1}{2008}\right)+1\)
\(B=\dfrac{2009}{2}+\dfrac{2009}{3}+...+\dfrac{2009}{2007}+\dfrac{2009}{2008}+\dfrac{2009}{2009}\)
\(B=2009.\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2007}+\dfrac{1}{2008}+\dfrac{1}{2009}\right)\)
\(\Rightarrow\dfrac{A}{B}=\dfrac{2009.\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2007}+\dfrac{1}{2008}+\dfrac{1}{2009}\right)}{\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2007}+\dfrac{1}{2008}+\dfrac{1}{2009}}=2009\)

I. Những kiến thức cần nắm vững
Văn bản thuyết minh nhằm cung cấp những tri thức về sự vật khách quan. Vì vậy bài viết (bài nói) cần chuẩn xác. Chuẩn xác là yêu cầu đầu tiên và cũng là yêu cầu quan trọng nhất đối với văn bản thuyết minh. Muốn chuẩn xác cần chú ý tìm hiểu thấu đáo trước khi viết; thu thập tài liệu tham khảo, chú ý đến thời điểm xuất bản của các tài liệu để có thể cập nhật những tìm tòi phát kiến mới cũng như thấy được những thay đổi thường có.
Thuyết minh bao giờ cũng có người đọc (người nghe). Bài viết vì thế cần tạo được hấp dẫn. Muốn làm cho văn bản hấp dẫn cần đưa ra những chi tiết cụ thể, sinh động, những con số chính xác; so sánh để làm nổi bật sự khác biệt, khắc sâu vào trí nhớ người đọc (người nghe); làm cho câu văn thuyết minh biến hoá linh hoạt; khi cần nên phối hợp nhiều loại kiến thức để đối tượng thuyết minh được soi rọi từ nhiều mặt
II. Trả lời câu hỏi
I- Bài luyện tập về tính chuẩn xác trong văn bản thuyết minh:
Trả lời các câu hỏi để kiểm tra tính chuẩn xác của văn bản thuyết minh (Nội dung câu hỏi, xem SGK).
a. Muốn biết lời thuyết minh về chương trình học có chuẩn xác hay không chỉ cần đối chiếu với mục lục sách Ngữ văn 10. Sau khi đối chiếu sẽ thấy lời thuyết minh không chuẩn xác vì:
- Chương trình Ngữ văn 10 không phải chỉ có văn học dân gian.
- Chương trình Ngữ văn 10 về văn học dân gian không phải chỉ có ca dao, tục ngữ.
- Chương trình Ngữ văn 10 không có câu đố.
b. Câu nêu ra trong SGK chưa chuẩn xác vì không phù hợp với ý nghĩa thực của những từ "thiên cổ hùng văn". "Thiên cổ hùng văn" là áng hùng văn của nghìn đời chứ không phải áng hùng văn viết trước đây một nghìn năm.
c. Văn bản dẫn trong bài tập không thể dùng để thuyết minh về nhà thơ Nguyễn Bỉnh Khiêm vì nội dung không nói đến Nguyễn Bỉnh Khiêm với tư cách nhà thơ.
II- Bài luyện tập về tính hấp dẫn của văn bản thuyết minh:
1. Đọc đoạn văn (SGK) và phân tích luận điểm: "Nếu bị tước đi môi trường kích thích, bộ não của đứa trẻ sẽ phải chịu đựng kìm hãm” trở nên cụ thể, dễ hiểu, hấp dẫn.
"Nếu bị tước đi môi trường kích thích, bộ não của đứa trẻ sẽ phải chịu đựng kìm hãm" là một luận điểm khái quát. Tác giả đã đưa ra hàng loạt những chi tiết cụ thể về bộ não của đứa trẻ ít được chơi đùa, ít được tiếp xúc và bộ não của con chuột bị nhốt trong hộp rỗng,... để làm sáng tỏ luận điểm. Luận điểm khái quát đã trở nên cụ thể, dễ hiểu. Vì vậy việc thuyết minh trở nên hấp dẫn, sinh động.
2. Đọc đoạn trích (SGK) và phân tích tác dụng tạo hứng thú của việc kể lại truyền thuyết về hòn đảo An Mạ.
Việc biết sự tích vua Lê trả kiếm cho Rùa thần tạo nên sự thích thú cho mọi người khi đứng trước Hồ Gươm. Chúng ta không chỉ thấy phong cảnh một Hồ Gươm trước mặt mà còn thấy một Hồ Gươm trong quá khứ, từ đó hiểu sâu về lịch sử, văn hoá, về đời sống tâm linh của dân tộc. Chính vì thế mà khi tham quan một thắng cảnh, một di tích nào ta cũng muốn biết những sự tích liên quan đến thắng cảnh, di tích ấy. Bài thuyết minh về Hồ Ba Bể đã trở nên hấp dẫn hơn khi tác giả nói đến những sự tích, những truyền thuyết giúp ta như trở về một thuở xa xưa thần tiên, kì ảo. Ngắm phong cảnh với những cảm xúc như thế, tâm hộn ta sẽ giàu có hơn, sâu sắc hơn.
III- Bài luyện tập chung:
Đọc đoạn trích tác phẩm “Miếng ngon Hà Nội” của nhà văn Vũ Bằng (SGK) và phân tích tính hấp dẫn của nó.
Đoạn văn thuyết minh của nhà văn Vũ Bằng hấp dẫn, sinh động vì:
- Tác giả sử dụng linh hoạt các kiểu câu: câu đơn, câu ghép, câu nghi vấn, câu cảm thán, câu khẳng định.
- Tác giả sử dụng những từ ngữ giàu hình tượng, giàu liên tưởng như: "Bó hành hoa xanh như lá mạ", "... một làn sương mỏng, mơ hồ như một bức tranh tàu vẽ những ông tiên ngồi đánh cờ ở trong rừng mùa thu",...
- Tác giả bộc lộ rất nhiều cảm xúc: "Trông mà thèm quá", "Có ai lại đừng vào ăn cho được”,...


Bài 10:
Đặt \(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}=k\)
=>\(\left\{{}\begin{matrix}c=dk\\b=ck=dk\cdot k=dk^2\\a=bk=dk^2\cdot k=dk^3\end{matrix}\right.\)
a:
\(\left(\dfrac{a+b+c}{b+c+d}\right)^3=\left(\dfrac{dk^3+dk^2+dk}{dk^2+dk+d}\right)^3=\left(\dfrac{dk\left(k^2+k+1\right)}{d\left(k^2+k+1\right)}\right)^3=k^3\)
\(\dfrac{a}{d}=\dfrac{dk^3}{d}=k^3\)
Do đó: \(\dfrac{a}{d}=\left(\dfrac{a+b+c}{b+c+d}\right)^3\)
b: Sửa đề: Chứng minh \(\dfrac{a^3+c^3+b^3}{c^3+b^3+d^3}=\dfrac{a}{d}\)
\(\dfrac{a^3+c^3+b^3}{c^3+b^3+d^3}=\dfrac{\left(dk^3\right)^3+\left(dk\right)^3+\left(dk^2\right)^3}{\left(dk\right)^3+\left(dk^2\right)^3+d^3}\)
\(=\dfrac{d^3k^9+d^3k^3+d^3k^6}{d^3k^3+d^3k^6+d^3}=\dfrac{d^3\cdot k^3\left(k^6+1+k^3\right)}{d^3\cdot\left(k^3+k^6+1\right)}=k^3\)
\(=\dfrac{dk^3}{d}=\dfrac{a}{d}\)