Bài 1. Cho tam giác ABC vuông tại A (AB < AC). C = α < 45°, đường trung tuyến AM, đường cao AH. MA=MB= MC = α. Chứng minh rằng:
a) sin 2α = 2sin α.cos α
b) 1+cos2α=2 cos² α
c) 1-cos 2α = 2sin α
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

định lý hàm số sin:
a/ \(\frac{a}{sinA}=\frac{b}{sinB}=\frac{c}{sinC}=\)2R
=> a = 2R.sinA = 2R.sin[180o - (B+C)] = 2R.sin(B+C)
và b = 2R.sinB; c = 2R.sinC thay vào (*) được:
\(\frac{2R\times sinB}{cosB}+\frac{2R\times sinC}{cosC}=\frac{2R\times sin\left(B+C\right)}{sinBsinC}\)
<=>sinB/cosB + sinC/cosC = sin(B+C)/(sinB.sinC)
<=> sin(B+C)/(cosBcosC) = sin(B+C)/(sinB.sinC)
<=> cosBcosC = sinB.sinC
<=> cosBcosC - sinB.sinC = 0
<=> cos(B+C) = 0
<=> B+C = 90o
vậy tam giác ABC vuông tại A

b/cosB+c/cosC=a/sinB.sinC (*)
Áp dụng định lý hàm số sin:
a/sinA = b/sinB = c/sinC = 2R
=> a = 2R.sinA = 2R.sin[1800 - (B+C)] = 2R.sin(B+C)
và b = 2R.sinB; c = 2R.sinC thay vào (*) được:
2R.sinB/cosB + 2RsinC/cosC = 2R.sin(B+C)/(sinB.sinC)
<=>sinB/cosB + sinC/cosC = sin(B+C)/(sinB.sinC)
<=> sin(B+C)/(cosBcosC) = sin(B+C)/(sinB.sinC)
<=> cosBcosC = sinB.sinC
<=> cosBcosC - sinB.sinC = 0
<=> cos(B+C) = 0
<=> B+C = 900

a) Do A + B + C = 180 độ nên góc A bù với góc B + C => sin(B + C) = sinA (sin hai góc bù bằng nhau)
(A + B)/2 + C/2 = 90 độ => hai góc (A + B)/2 và C/2 là hai góc phụ nhau => cos (A + B)/2 = sin(C/2) (Chắc đề bài bạn cho nhầm thành sinC)
b) Bạn xem lại đề nhé
c) \(sin^6a+cos^6a+3sin^2a.cos^2a=\left(sin^2a\right)^3+\left(cos^2a\right)^3+3.sin^2a.cos^2a\)
= \(\left(sin^2a+cos^2a\right)\left(sin^4a+cos^4a-sin^2a.cos^2a\right)+3sin^2a.cos^2a\)
= \(sin^4a+cos^4a+2sin^2a.cos^2a\)
= \(\left(sin^2a+cos^2a\right)^2=1\)

a) Theo định lý sin: \(\frac{a}{{\sin A}} = \frac{b}{{\sin B}} \to b = \frac{{a.\sin B}}{{\sin A}}\) thay vào \(S = \frac{1}{2}ab.\sin C\) ta có:
\(S = \frac{1}{2}ab.\sin C = \frac{1}{2}a.\frac{{a.\sin B}}{{\sin A}}.sin C = \frac{{{a^2}\sin B\sin C}}{{2\sin A}}\) (đpcm)
b) Ta có: \(\hat A + \hat B + \hat C = {180^0} \Rightarrow \hat A = {180^0} - {75^0} - {45^0} = {60^0}\)
\(S = \frac{{{a^2}\sin B\sin C}}{{2\sin A}} = \frac{{{{12}^2}.\sin {{75}^0}.\sin {{45}^0}}}{{2.\sin {{60}^0}}} = \frac{{144.\frac{1}{2}.\left( {\cos {{30}^0} - \cos {{120}^0}} \right)}}{{2.\frac{{\sqrt 3 }}{2}\;}} = \frac{{72.(\frac{{\sqrt 3 }}{2}-\frac{{-1 }}{2}})}{{\sqrt 3 }} = 36+12\sqrt 3 \)

Đặt \(m=2018,\frac{\sin B+m\sin C}{m\cos B+\cos C}=\sin A\Leftrightarrow b+mc=a\left(m\cos B+\cos C\right)\)
\(\Leftrightarrow b+mc=\frac{m\left(a^2+c^2-b^2\right)}{2c}+\frac{a^2+b^2-c^2}{2b}\)
\(\Leftrightarrow2bc\left(b+mc\right)=mb\left(a^2+c^2-b^2\right)+c\left(a^2+b^2-c^2\right)\)
\(\Leftrightarrow2b^2c+2mbc^2=mba^2+mbc^2-mb^3+ca^2+cb^2-c^3\)
\(\Leftrightarrow\left(c+mb\right)\left(b^2+c^2-a^2\right)=0\Leftrightarrow a^2=b^2+c^2\)
Vậy tam giác ABC vuông tại A
Dễ dàng CM được \(S_{ABC}=6.S_{MBG}\Rightarrow bc=12.S_{MBG}\).Do vậy ta cần CM bc chia hết cho 12
( ta sử dụng tính chất của số chính phương)
- Số chính phương chia 3 chỉ dư 0 hoặc 1
- Số chính phương chia 4 chỉ dư 0 hoặc 1
- Số chính phương lẻ chia 8 chỉ dư 1
*) Ta thấy trong 2 số \(b^2,c^2\)có ít nhất 1 số chia hết cho 3. giả sử không có số nào trong 2 số đó chia hết cho 3. Khi đó mỗi số đều chia 3 dư 1. Do đó a2 chia 3 dư 2 ( trái với tính chất số chính phương)
Do 3 là số nguyên tố nên trong 2 số b,c có ít nhất 1 số chia hết cho 3 . (1)
*)Chứng minh trong 2 số b,c có ít nhất 1 số chia hết cho 4. giả sử không có số nào trong 2 số đó chia hết cho 4. Khi đó \(b=4m+r;c=4n+q;r,q\in\left\{1;2;-1\right\}\)
+ Nếu \(r,q\in\left\{1;-1\right\}\Rightarrow a^2\)chia 4 dư 2 ( vô lý)
+ Nếu \(r\in\left\{-1;1\right\},q=2\) hoặc ngược lại thì a2 là số lẻ và a2 chia 8 dư 5 ( vô lý)
+ Nếu r=q=2 thì \(a^2=4\left(2m+1\right)^2+4\left(2n+1\right)^2\Rightarrow\)a chẵn
Đặt \(a=2p\Rightarrow p^2=\left(2m+1\right)^2+\left(2n+1\right)^2\Rightarrow p^2\)chia 4 dư 2 ( vô lý)
Vậy trong 2 số b,c có ít nhất 1 số chia hết cho 4 (2)
Từ (1) và (2) => đpcm
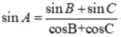
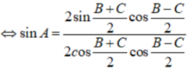
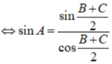
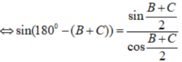
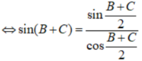
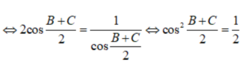
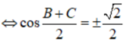
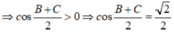
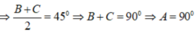
a: Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MB=MC
Xét ΔMAC có \(\widehat{AMB}\) là góc ngoài tại M
nên \(\widehat{AMB}=\widehat{MAC}+\widehat{MCA}=2\cdot\widehat{ACB}=2\alpha\)
=>\(sin2\alpha=sinAMB=\dfrac{AH}{AM}=AH:\dfrac{BC}{2}=\dfrac{2AH}{BC}\)
Xét ΔAHC vuông tại H có \(sinC=\dfrac{AH}{AC}\)
Xét ΔABC vuông tại A có \(cosC=\dfrac{AC}{BC}\)
\(2sin\alpha\cdot cos\alpha=2\cdot\dfrac{AH}{AC}\cdot\dfrac{AC}{BC}=\dfrac{2\cdot AH}{BC}\)
Do đó: \(sin2\alpha=2\cdot sin\alpha\cdot cos\alpha\)
b: \(cos2\alpha=cosAMH=\dfrac{HM}{AM}\)
=>\(1+cos2\alpha=1+\dfrac{HM}{AM}=\dfrac{HC}{AM}=\dfrac{2\cdot HC}{BC}=2\cdot\dfrac{AC^2}{BC^2}\)
\(2\cdot cos^2\alpha=2\cdot cos^2C=2\cdot\left(\dfrac{CA}{BC}\right)^2=2\cdot\dfrac{CA^2}{CB^2}\)
Do đó: \(1+cos2\alpha=2\cdot cos^2\alpha\)
c: \(1-cos2\alpha=1-cosAMH=1-\dfrac{HM}{AM}=\dfrac{HB}{AM}=\dfrac{2HB}{BC}=2\cdot\dfrac{AB^2}{BC^2}\)
\(2\cdot sin^2\alpha=2\cdot sin^2ACB=2\cdot\left(\dfrac{AB}{BC}\right)^2\)
Do đó: \(1-cos2a=2\cdot sin^2\alpha\)