Viết các số có 6 chữ số sao cho mỗi số chỉ được lập từ 3 chữ số 0 và 3 chữ số 1?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 10 2015
1) Gọi d = ƯCLN của tất cả các số lập được từ 6 chữ số trên
=> Hiệu hai số bất kì trong đó cũng chia hết cho d
Ta có: 123465 - 123456 = 9 => 9 chia hết cho d => d có thể bằng 1; 3; 9
Mà Tổng các chữ số của mỗi số lập được đều bằng 1 + 2+ 3+ 4+5+6 = 21 => Các số đó chia hết cho 3, không chia hết cho 9
=> d = 3
Vậy ƯCLN của các số lập được bằng 3
2)
+) Nếu các chữ số a; b đã cho đều khác 0 thì từ các chữ số a; b; 5; 8 ta sẽ lập được 24 số, vì
- Có 4 cách chọn chữ số hàng nghìn
- Có 3 cách chọn chữ số hàng trăm
- Có 2 cách chọn chữ số hàng chục
- Có 1 cách chọn chữ số hàng đơn vị
=> có tất cả là: 4 x 3 x 2 x 1 = 24 số
Theo đề bài, chỉ lập được 18 số nên trong a; b có 1 chữ số bằng 0. Coi b = 0
+) Ta lập được 18 số là:
a058; a085; a508; a580; a850;a805
50a8;508a; 580a;58a0;5a80;5a08
85a0;850a;80a5;805a;8a50;8a05
Trong 18 số trên, ta thấy: Chữ số a; 5; 8 đều xuất hiện ở hàng nghìn 6 lần; và a; 0;5;8 đều xuất hiện ở mỗi hàng trăm; chục ; đơn vị 4 lần
Theo phân tích cấu tạo số ta có: Tổng 18 số trên là:
(a + 5 + 8) x 6 x 1000 + (a + 0 + 5 + 8) x 4 x 100 + (a + 0 + 5 + 8) x 4 x 10 + (a + 0 + 5 + 8) x 4 x 1 = (a+13) x 6444
Theo bài cho ta có: (a+13) x 6444 = 90 216
=> a+ 13 = 90 216 : 6444 = 13 => a = 1
Vậy a = 1; b = 0 (hoặc a = 0 ; b = 1)
LV
14 tháng 3
mỗi số có 6 lần giá trị nghìn và 2 lần giá trị trăm, chục, đơn vị
ta có số 5 và 8 là các giá trị đã biết
5=
(6 x 5000)+(2 x 500)+(2 x 50)+(2 x 5)=31110
tương tự với 8
8=49776
49776+31110=80886
theo đề bài tổng là 90216
90216 - 80886= 9330
=> (6 x 1000)+(2 x 100)+(2 x 10)+(2 x 1)=6222
vậy a và b không lớn hơn 1
0= 3108
6222+3108 = 9330
=> a=0 b=1
3 tháng 8 2021
Bài 6
Chọn chữ số 1 ở hàng chục nghìn ta lập được 24 số
Tương tự nên ta lập được
24 x 5 = 120 (số)
Tổng là:
(1 + 2 + 3 + 4 + 5) x 10000 x 24 + (1 + 2 + 3 + 4 + 5) x 1000 x 24 + (1 + 2 + + 3 + 4 + 5) x 100 x 24 + (1 + 2 + 3 + 4 + 5) x 10 x 24 + (1 + 2 + 3 + 4 + 5) x x 1 x 24
= (1 + 2 + 3 + 4 + 5) x 24 x 11111
= 15 x 24 x 11111 = 3999960
3 tháng 8 2021
Bài 6:
Ta lập được 3 số 334, 343, 433
Tổng các số:
(3 + 3 + 4) x 100 x 1 + (3 + 3 + 4) x 10 + (3 + 3 + 4) x 1
= 10 x (10 + 10 + 1)
= 10 x 111 = 1110
.
CM
8 tháng 9 2017
Gọi số cần lập 
Bước 1: Xếp chữ số 0 vào 1 trong 5 vị trí từ a2 đến a6, có 5 cách xếp.
Bước 2: Xếp chữ số 1 vào 1 trong 5 vị trí còn lại (bỏ 1 vị trí chữ số 0 đã chọn), có 5 cách xếp.
Bước 3: Chọn 4 chữ số trong 8 chữ số {2, 3, 4, 5, 6 , 7, 8, 9}để xếp vào 4 vị trí còn lại, có 
cách.
Theo quy tắc nhân có 
số thỏa yêu cầu.
Chọn D.
16 tháng 9 2015
Các số là:
2035;2053;2305;2350;2503;2530;3025;3052;3205;3250;3502;3520;5023;5032;5203;5230;5302;5320
2035+2053+2305+2350+2503+2530+3025+3052+3205+3250+3502+3520+5023+5032+5203+5230+5302+5320=44563
CM
18 tháng 8 2017
Chọn C
Ta có thể chia làm bốn trường hợp sau
TH1: Số 5 có mặt một lần, số 6 có mặt một lần.( Bao gồm các khả năng sau: mỗi số có mặt một lần hoặc một số 5, một số 6 hai số 3 hoặc một số 5, một số 6 hai số 4)
Số các số được tạo thành là: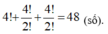 
TH2: Số 5 có mặt một lần, số 6 không có mặt.
Số các số được tạo thành là: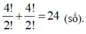 
TH3: Số 6 có mặt một lần, số 5 không có mặt.
Số các số được tạo thành là: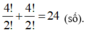 
TH4: Số 5 và số 6 không có mặt.( Số 3 và số 4 mỗi số có mặt đúng hai lần)
Số các số được tạo thành là: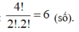 
Vậy có thể lập được 102 số thỏa mãn đề bài.
`100011;100101;101001;110001;100110;101010;110010;101100;110100`
và 111000