Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Gọi số có 3 chữ số cần tìm là a b c ¯
trong đó a , b , c ∈ 2 ; 3 ; 4 ; 5 ; 6 ; 7
Chọn a có 6 cách, chọn b có 6 cách, chọn c có 6 cách
Số các số có 3 chữ số được lập thành là 6.6.6=216(số)

Chọn C
Ta có thể chia làm bốn trường hợp sau
TH1: Số 5 có mặt một lần, số 6 có mặt một lần.( Bao gồm các khả năng sau: mỗi số có mặt một lần hoặc một số 5, một số 6 hai số 3 hoặc một số 5, một số 6 hai số 4)
Số các số được tạo thành là: 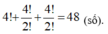
TH2: Số 5 có mặt một lần, số 6 không có mặt.
Số các số được tạo thành là: 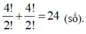
TH3: Số 6 có mặt một lần, số 5 không có mặt.
Số các số được tạo thành là: 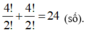
TH4: Số 5 và số 6 không có mặt.( Số 3 và số 4 mỗi số có mặt đúng hai lần)
Số các số được tạo thành là: 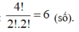
Vậy có thể lập được 102 số thỏa mãn đề bài.

Đáp án A
Số cách lập số tự nhiên gồm 3 chữ số khác nhau từ 6 chữ số là A 6 3 = 120

Chọn A
Tập hợp các chữ số chẵn chọn từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 là {0,2,4,6}.
Tập hợp các chữ số lẻ chọn từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 là {1,3,5,7}.
Ta có,
+ Số các tự nhiên có 5 chữ số đôi một khác nhau sao cho có đúng 3 chữ số chẵn và 2 chữ số lẻ có dạng
a
b
c
d
e
¯
(a có thể bằng 0) là ![]() .
.
+ Số các tự nhiên có 5 chữ số đôi một khác nhau sao cho có đúng 3 chữ số chẵn và 2 chữ số lẻ có dạng
0
b
c
d
e
¯
là ![]()
Suy ra, số các số tự nhiên thỏa đề ra là ![]() .
.
Ý tưởng phát triển câu 39: thêm ràng buộc về thứ tự sắp xếp cho số tự nhiên lập được.

Đáp án là A.
Gọi số cần lập có dạng: a 1 a 2 a 3 a 4 a 5
• Chọn 2 số lẻ thuộc nhóm {1 ;3 ;5 ;7} ⇒ C 4 2
• Chọn 3 số chẳn trong nhóm {0;2;4;6} ⇒ C 4 3
• Hoán vị 2 nhóm trên có 5! cách
* Các số có số a1 = 0
• Chọn 2 số lẻ thuộc nhóm {1 ;3 ;5 ;7} ⇒ C 4 2
• Chọn 2 số chẳn trong nhóm {0;2;4;6} ⇒ C 3 2
• Hoán vị 2 nhóm trên có 4! cách
Vậy các số cần tìm: C 4 2 . C 4 3 . 5 ! - C 4 2 . C 3 2 . 4 ! = 2448 số

Lời giải:
Gọi số thỏa mãn đề là $M$
Có $C^2_5$ cách chọn ra 2 số lẻ từ tập A
Với mọi cách chọn, có $A^2_5$ cách xếp 2 số lẻ đó trong $M$
Ba chữ số còn lại từ $(2;4;6;8)$ có $A^3_4$ cách chọn
Vậy số chữ số thỏa mãn: $C^2_5.A^2_5.A^3_4=4800$ số
