tìm x là số nguyên để 3-x/3+x nhận giá trị nguyên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: x + 1 x - 3 = x - 3 + 4 x - 3 = 1 + 4 x - 3
Để 1 + 4 x - 3 nhận giá trị nguyên thì 4 x - 3 phải có giá trị nguyên. Vì x nguyên nên √x là số nguyên hoặc số vô tỉ.
* Nếu x là số vô tỉ thì x - 3 là số vô tỉ nên 4 x - 3 không có giá trị nguyên. Trường hợp này không có giá trị nào của x để biểu thức nhận giá trị nguyên.
* Nếu
x
là số nguyên thì
x
- 3 là số nguyên. Vậy để 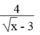 nguyên thì
x
- 3 phải là ước của 4.
nguyên thì
x
- 3 phải là ước của 4.
Đồng thời x ≥ 0 suy ra: x ≥ 0
Ta có: W(4) = {-4; -2; -1; 1; 2; 4}
Suy ra: x - 3 = -4 ⇒ x = -1 (loại)
x - 3 = -2 ⇒ x = 1 ⇒ x = 1
x - 3 = -1 ⇒ x = 2 ⇒ x = 4
x - 3 = 1 ⇒ x = 4 ⇒ x = 16
x - 3 = 2 ⇒ x = 5 ⇒ x = 25
x - 3 = 4 ⇒ x = 7 ⇒ x = 49
Vậy với x ∈ {1; 4; 16; 25; 49} thì biểu thức x + 1 x - 3 nhận giá trị nguyên.

a) Ta có: \(M=\dfrac{8x+1}{4x-5}=\dfrac{8x-10+11}{4x-5}=\dfrac{2\left(x-5\right)+11}{4x-5}=2+\dfrac{11}{4x-5}\)
Để M nhận giá trị nguyên thì \(2+\dfrac{11}{4x-5}\) nhận giá trị nguyên
\(\Rightarrow\dfrac{11}{4x-5}\) nhận giá trị nguyên
\(\Rightarrow11⋮4x-5\)
Vì \(x\in Z\) nên \(4x-5\in Z\)
\(\Rightarrow4x-5\inƯ\left(11\right)=\left\{\pm1;\pm11\right\}\)
\(\Rightarrow x\in\left\{1;\pm1,5;4\right\}\)
Vậy \(x\in\left\{1;4\right\}\) thỏa mãn \(x\in Z\).
b) Ta có: \(A=\dfrac{5}{4-x}\). ĐK: \(x\ne4\)
Nếu 4 - x < 0 thì x > 4 \(\Rightarrow A>0\)
4 - x > 0 thì x < 4 \(\Rightarrow A< 0\)
Để A đạt GTLN thì 4 - x là số nguyên dương nhỏ nhất
\(\Rightarrow4-x=1\Rightarrow x=3\)
\(\Rightarrow A=\dfrac{5}{4-3}=5\)
Vậy MaxA = 5 tại x = 3
c) \(B=\dfrac{8-x}{x-3}\). ĐK: \(x\ne3\).
Ta có: \(B=\dfrac{8-x}{x-3}=\dfrac{-\left(x-8\right)}{x-3}=\dfrac{-\left(x-3\right)+5}{x-3}=\dfrac{5}{x-3}-1\)
Để B đạt giá trị nhỏ nhất thì \(\dfrac{5}{x-3}-1\) nhỏ nhất
\(\Rightarrow\dfrac{5}{x-3}\) nhỏ nhất
Nếu x - 3 > 0 thì x > 3 \(\Rightarrow\dfrac{5}{x-3}>0\)
x - 3 < 0 thì x < 3 \(\Rightarrow\dfrac{5}{x-3}< 0\)
Để \(\dfrac{5}{x-3}\) nhỏ nhất thì x - 3 là số nguyên âm lớn nhất
\(\Rightarrow x-3=-1\Rightarrow x=2\)
\(\Rightarrow B=\dfrac{8-2}{2-3}=-6\)
Vậy MaxB = -6 tại x = 2.
Mình làm sai câu a...
Ta có: \(M=\dfrac{8x+1}{4x-1}=\dfrac{8x-2+3}{4x-1}=\dfrac{2\left(4x-1\right)+3}{4x-1}=2+\dfrac{3}{4x-1}\)
Để M nhận giá trị nguyên thì \(2+\dfrac{3}{4x-1}\) nhận giá trị nguyên
\(\Rightarrow\dfrac{3}{4x-1}\) nhận giá trị nguyên
Vì \(4x-1\in Z\) nên \(4x-1\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
\(\Rightarrow x\in\left\{\pm0,5;0;1\right\}\)
Vậy \(x\in\left\{0;1\right\}\) thỏa mãn \(x\in Z\).

ĐKXĐ : \(x\ne2\)
Ta có HĐT sau (a - b)(a + b) = a2 - ab + ab - b2 = a2 - b2
Áp dụng vào bài toán ta có:
x4 + 3 = (x4 - 16) + 19
= [(x2)2 - 42] + 19
= (x2 - 4)(x2 + 4) + 19
= (x - 2)(x + 2)(x2 + 4) + 19
Từ đó \(A=\dfrac{x^2+3}{x-2}=\dfrac{\left(x-2\right).\left(x+2\right).\left(x^2+4\right)+19}{x-2}\)
\(=\left(x+2\right).\left(x^2+4\right)+\dfrac{19}{x-2}\)
Do \(x\inℤ\) nên \(A\inℤ\Leftrightarrow19⋮x-2\)
\(\Leftrightarrow x-2\inƯ\left(19\right)=\left\{1;-1;19;-19\right\}\)
hay \(x\in\left\{3;1;21;-17\right\}\)

Ta có : B = 2x+1/x-3 = (2x-6)+7/x-3 = 2+ 7/x-3
Để B nhận giá trị nguyên thì x-3 thuộc Ư(7) = (+-1;+-7)
suy ra : x-3=-1 => x=2 x-3=1 => x=4
x-3=-7 => x=-4 x-3=7 => x=10
Vậy x =(-4;2;4;10) thì B nhận giá trị nguyên

a: Thay x=-4 vào B, ta được:
\(B=\dfrac{-4+3}{-4}=\dfrac{-1}{-4}=\dfrac{1}{4}\)
b: \(P=A\cdot B=\dfrac{x^2-3x+2x-9+3x+9}{\left(x-3\right)\left(x+3\right)}\cdot\dfrac{x+3}{x}\)
\(=\dfrac{x^2+2x}{\left(x-3\right)}\cdot\dfrac{1}{x}=\dfrac{x+2}{x-3}\)
c: Để P nguyên thì \(x-3\in\left\{1;-1;5;-5\right\}\)
hay \(x\in\left\{4;2;8;-2\right\}\)

1 - 2x = -(2x - 1)
= -(2x + 6 - 7)
= -(2x + 6) + 7
= -2(x + 3) + 7
Để B nguyên thì (1 - 2x) ⋮ (x + 3)
⇒ 7 ⋮ (x + 3)
⇒ x + 3 ∈ Ư(7) = {-7; -1; 1; 7}
⇒ x ∈ {-10; -4; -2; 4}

Lời giải:
Để $A$ nguyên thì \(x-3\vdots 2x+3\)
\(\Leftrightarrow 2(x-3)\vdots 2x+3\)
\(\Leftrightarrow 2x-6\vdots 2x+3\Leftrightarrow 2x+3-9\vdots 2x+3\)
\(\Leftrightarrow 9\vdots 2x+3\Rightarrow 2x+3\in\left\{\pm 1;\pm 3;\pm 9\right\}\)
\(\Rightarrow x\in \left\{-2; -1; 0; -3; -6; 3\right\}\)

a) x khác 2
b) với x<2
c) \(A=\frac{x\left(x-2\right)+2\left(x-2\right)+7}{x-2}=x+2+\frac{7}{x-2}\)
x-2=(-7,-1,1,7)
x=(-5,1,3,9)
a) đk kiện xác định là mẫu khác 0
=> x-2 khác o=> x khác 2
b)
tử số luôn dương mọi x
vậy để A âm thì mẫu số phải (-)
=> x-2<0=> x<2
c)thêm bớt sao cho tử là các số hạng chia hết cho mẫu
cụ thể
x^2-2x+2x-4+4+3
ghép
x(x-2)+2(x-2)+7
như vậy chỉ còn mỗi số 7 không chia hết cho x-2
vậy x-2 là ước của 7=(+-1,+-7) ok
Ta có:
\(\dfrac{3-x}{3+x}=\dfrac{-x+3}{x+3}=\dfrac{-\left(x+3\right)+6}{x+3}=-1+\dfrac{6}{x+3}\)
Để biểu thức nhận giá trị nguyên thì: 6 ⋮ x + 3
=> x + 3 ∈ Ư(6) = {1; -1; 2; -2; 3; -3; 6; -6}
=> x ∈ {-2; -4; -1; -5; 0; -6; 3; -9}