K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 3 2022
a: Ta có: ΔCAB cân tại C
mà CI là đường cao
nên I là trung điểm của AB
hay IA=IB
b: Xét ΔCHI vuông tại H và ΔCKI vuông tại K có
CI chung
\(\widehat{HCI}=\widehat{KCI}\)
Do đó; ΔCHI=ΔCKI
Suy ra: IH=IK
c: AB=12cm nên IA=6cm
=>IC=8cm
16 tháng 3 2022
a) Xét hai Δ vuông ACI và Δ BCI ta có:
CICI chung
AC=BCAC=BC
Góc AICAIC=Góc BICBIC=90oo
⇒ Δ ACI=ΔBCIACI=ΔBCI (ch-cgv)
⇒ IA=IBIA=IB (hai cạnh tương ứng bằng nhau)
b) Do `CA=CB=10cmnênnênΔ ABCcânđỉnhCnêngóccânđỉnhCnêngócCAB=gócgócCBA`
hay góc HAIHAI=góc KBIKBI
Xét Δ vuông IHAIHA và Δ IKBIKB có:
IA=IBIA=IB (chứng minh trên)
góc HAIHAI=góc KBIKBI
Góc AHI=BKI=90o90o
⇒ Δ IHAIHA = Δ IKBIKB (ch-gn)
⇒IH=IKIH=IK (hai cạnh tương ứng bằng nhau)
c) IA=IBIA=IB=122122=66
Áp dụng định lý Pytago vào Δ vuông ACI có:
AC²=AI²+IC²AC²=AI²+IC²
⇒ IC²=AC²−AI²=10²−6²=64IC²=AC²-AI²=10²-6²=64
⇒ IC=8
HQ
Hà Quang Minh
Giáo viên
8 tháng 9 2023
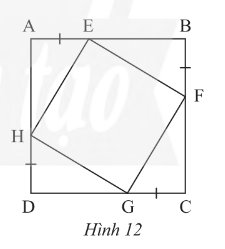
a) Vì \(ABCD\) là hình vuông nên \(AB = BC = CD = DA\); \(\widehat A = \widehat B = \widehat C = \widehat D = 90^\circ \)
Mà \(AE = BF = CG = HD\) (gt) suy ra \(BE = CF = DG = AH\)
Xét \(\Delta AEH\) và \(\Delta DHG\) ta có:
\(\widehat {\rm{A}} = \widehat {\rm{D}} = 90\)
\(AE = GH\) (gt)
\(AH = DG\) (gt)
Suy ra \(\Delta AEH = \Delta DHG\) (c-g-c)
Suy ra \(\widehat {{\rm{AEH}}} = \widehat {{\rm{DHG}}}\) (hai góc tương ứng)
Mà \(\widehat {AEH} + \widehat {AHE} = 90^\circ \)
Suy ra \(\widehat {DHG} + \widehat {AHE} = 90^\circ \)
Suy ra \(\widehat {EHG} = 90^\circ \)
Chứng minh tương tự ta được \(\widehat {HGF} = 90^\circ ;\;\widehat {GFE} = 90^\circ \)
Vậy tứ giác \(EFGH\) là một góc vuông
b) Vì \(\Delta AEH = \Delta DHG\) (cmt)
Suy ra \(HE = HG\) (2)
Từ (1) và (2) suy ra \(EFGH\) là hình vuông
c) chứng minh tương tự câu b ta có: \(HE = EF\); \(HE = FG\)
Khi đó \(EFGH\) có \(HE = HG = EF = FG\) nên là hình thoi (3)
Tứ giác \(EFGH\) có ba góc vuông nên là hình chữ nhật (4)
Từ (3) và (4) suy ra \(EFGH\) là hình vuông
19 tháng 1 2017
a) vì OT là tia phân giác của xoy nên xot =yot , i thuộc ot từ i ta kẻ hai đoạn ik và ih .
ih nằm trong góc xot và ih vuông góc với ox.ik nằm trong góc yot và ik vuông góc với oy. Nên ih=ik.
câu 3 mk chịu bn hỏi thầy cô nha! Nhớ k cho mk nha!
10 tháng 4 2018
a) vì OT là tia phân giác của xoy nên xot =yot ,
i thuộc ot từ i ta kẻ hai đoạn ik và ih .
ih nằm trong góc xot và ih vuông góc với ox.ik nằm trong góc yot và ik vuông góc với oy.
Nên ih=ik.
8 tháng 11 2021
a: Xét tứ giác AHIK có
\(\widehat{AHI}=\widehat{AKI}=\widehat{KAH}=90^0\)
Do đó: AHIK là hình chữ nhật
14 tháng 3 2021
Xét tam giác MNI và MPI có
MI là cạnh chung
MN = MP( tam giác MNP cân)
Góc MIN = góc MIP = 90°
=> Tam giác MIN = tam giác MIP( cgv - ch)
IN = IP = 5 cm nên I là trung điểm của NP
b) Tam giác MIN vuông tại I có
NI2 + MI2 = MN2( định lí Pytago)
MI2 + 52 = 142
MI2 + 25 = 196
MI2 = 144
MI=12
c) Xét tam giác PHI và PKI có
MI là cạnh chung
Góc HMI = KMI ( tam giác NMI = PMI )
Góc IHM = IKM = 90°
=》 Tam giác HMI = KMI ( ch - gn)
=》IH=IK
31 tháng 1 2021
a) Xét ΔABI và ΔACI có
AB=AC(ΔABC cân tại A)
AI chung
BI=CI(I là trung điểm của BC)
Do đó: ΔABI=ΔACI(c-c-c)
nên \(\widehat{BAI}=\widehat{CAI}\)(hai góc tương ứng)
mà tia AI nằm giữa hai tia AB,AC
nên AI là tia phân giác của \(\widehat{BAC}\)(đpcm)
b) Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: IB=IC(I là trung điểm của BC)
nên I nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AI là đường trung trực của BC
hay AI\(\perp\)BC(đpcm)
c) Xét ΔIHB vuông tại H và ΔIKC vuông tại K có
IB=IC(I là trung điểm của BC)
\(\widehat{HBI}=\widehat{KCI}\)(hai góc ở đáy của ΔABC cân tại A)
Do đó: ΔIHB=ΔIKC(cạnh huyền-góc nhọn)
nên IH=IK(hai cạnh tương ứng)
d) Xét ΔABI vuông tại I và ΔDCI vuông tại I có
IB=IC(I là trung điểm của BC)
IA=ID(gt)
Do đó: ΔABI=ΔDCI(hai cạnh góc vuông)
nên \(\widehat{ABI}=\widehat{DCI}\)(hai góc tương ứng)
mà \(\widehat{ABI}\) và \(\widehat{DCI}\) là hai góc ở vị trí so le trong
nên AB//CD(Dấu hiệu nhận biết hai đường thẳng song song)
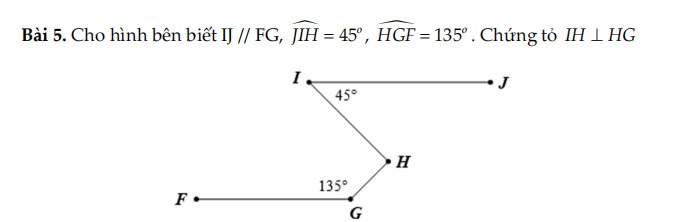
Kẻ H\(x\) // FG
Ta có : \(\widehat{xHI}\) = \(\widehat{JIH}\) = 450 (Hai góc so le trong)
\(\widehat{xHG}\) + \(\widehat{FGH}\) = 1800 (hai góc trong cùng phía)
⇒ \(\widehat{xHG}\) = 1800 - 1350 = 450
\(\widehat{IGH}\) = \(\widehat{xHG}\) + \(\widehat{xHI}\) = 450 + 450 = 900
Vậy HG vuông góc với HI