K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
31 tháng 7 2017
Đáp án C
Lời giải trên là sai. Cách làm lời giải này chỉ đúng đối với bài toán tìm giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên một đoạn .
Để giải bài toán này, ta lập bảng biến thiên của hàm số y = 2 x 4 − 4 x 2 + 3 trên R
* Bước 1: Tập xác định D = ℝ . Đạo hàm y ' = 8 x 3 − 8 x .
* Bước 2: Cho y ' = 0 tìm x = 0 ; x = − 1 ; x = 1 .
* Bước 3: Ta có bảng biến thiên sau:
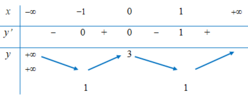
Quan sát bảng biến thiên, ta thấy giá trị nhỏ nhất của hàm số là 1 và hàm số không có giá trị lớn nhất. Vậy lời giải trên sai từ bước 3.
CM
28 tháng 1 2019
Đáp án C
Lưu ý: Đề không cho tìm max – min trên đoạn nên ta không thể so sánh các giá trị như vậy
Cách giải: Lập BBT và ở đây kết luận được giá trị nhỏ nhất của hàm số là 1 , nhưng hàm số không có giá trị lớn nhất.
6 tháng 11 2016
bài 2
Ta có:
\(A=\left|x-102\right|+\left|2-x\right|\Rightarrow A\ge\left|x-102+2-x\right|=-100\Rightarrow GTNNcủaAlà-100\)đạt được khi \(\left|x-102\right|.\left|2-x\right|=0\)
Trường hợp 1: \(x-102>0\Rightarrow x>102\)
\(2-x>0\Rightarrow x< 2\)
\(\Rightarrow102< x< 2\left(loại\right)\)
Trường hợp 2:\(x-102< 0\Rightarrow x< 102\)
\(2-x< 0\Rightarrow x>2\)
\(\Rightarrow2< x< 102\left(nhận\right)\)
Vậy GTNN của A là -100 đạt được khi 2<x<102.
NT
1
AH
Akai Haruma
Giáo viên
23 tháng 1 2017
Lời giải:
Áp dụng BĐT Am-Gm:
\(\frac{3(x+y)}{2}.\frac{3(x+y)}{2}.(x+2z).(y+2z)\leq \left(\frac{3x+3y+x+2z+y+2z}{4}\right)^4=(x+y+z)^4\)
\(\Rightarrow \frac{4}{(x+y)\sqrt{(x+2z)(y+2z)}}=\frac{6}{\sqrt{\left ( \frac{3}{2} \right )^2(x+y)^2(x+2z)(y+2z)}}\geq\frac{6}{(x+y+z)^2}(1)\)
Tương tự \(\frac{5}{(y+z)\sqrt{(y+2x)z+2x)}}\geq \frac{15}{2(x+y+z)^2}(2)\)
Mặt khác, áp dụng BĐT Cauchy-Schwarz:
\((x^2+y^2+z^2+4)(1+1+1+1)\geq (x+y+z+2)^2\Rightarrow \frac{4}{\sqrt{x^2+y^2+z^2+4}}\leq \frac{8}{x+y+z+2}(3)\)
Từ \((1),(2),(3)\Rightarrow P\leq \frac{8}{x+y+z+2}-\frac{27}{2(x+y+z)^2}\)
Đặt \(x+y+z=t\). Ta sẽ đi tìm max của \(f(t)=\frac{8}{t+2}-\frac{27}{2t^2}\)
Có \(f'(t)=\frac{27}{t^3}-\frac{8}{(t+2)^2}=0\Leftrightarrow t=6\)\(\Rightarrow f(t)_{\max}=f(6)=\frac{5}{8}\)
\(\Rightarrow P_{\max}=\frac{5}{8}\). Dấu $=$ xảy ra khi $x=y=z=2$
22 tháng 7 2016
a) gtnn bạn ạ
GTNN A= -4 vì 2/3x-1/ >= 0
b) gtln bạn ạ
GTLN B = 10 vì 4/x-2/ >=0
7 tháng 1 2020
các bạn trả lời nhanh giúp mình nhé, ngày mai cô kiểm tra rồi
Bài 7:
\(\dfrac{x-2}{5}=\dfrac{-2}{2y+1}\)
=>\(\left(x-2\right)\left(2y+1\right)=5\cdot\left(-2\right)=-10\)
mà 2y+1 lẻ
nên \(\left(x-2;2y+1\right)\in\left\{\left(10;-1\right);\left(-10;1\right);\left(2;-5\right);\left(-2;5\right)\right\}\)
=>\(\left(x;y\right)\in\left\{\left(12;-1\right);\left(-8;0\right);\left(4;-3\right);\left(0;2\right)\right\}\)
Bài 6:
\(\dfrac{1}{20}+\dfrac{1}{44}+\dfrac{1}{70}+...+\dfrac{2}{x\left(x+3\right)}=\dfrac{101}{770}\)
=>\(\dfrac{2}{40}+\dfrac{2}{88}+\dfrac{2}{140}+...+\dfrac{2}{x\left(x+3\right)}=\dfrac{101}{770}\)
=>\(\dfrac{2}{3}\left(\dfrac{3}{5\cdot8}+\dfrac{3}{8\cdot11}+...+\dfrac{3}{x\left(x+3\right)}\right)=\dfrac{101}{770}\)
=>\(\dfrac{2}{3}\left(\dfrac{1}{5}-\dfrac{1}{8}+\dfrac{1}{8}-\dfrac{1}{11}+...+\dfrac{1}{x}-\dfrac{1}{x+3}\right)=\dfrac{101}{770}\)
=>\(\dfrac{2}{3}\left(\dfrac{1}{5}-\dfrac{1}{x+3}\right)=\dfrac{101}{770}\)
=>\(\dfrac{1}{5}-\dfrac{1}{x+3}=\dfrac{101}{770}:\dfrac{2}{3}=\dfrac{101}{770}\cdot\dfrac{3}{2}=\dfrac{303}{1540}\)
=>\(\dfrac{1}{x+3}=\dfrac{1}{5}-\dfrac{303}{1540}=\dfrac{1}{308}\)
=>x+3=308
=>x=305
Bài 8:
a: \(\left(2x-1\right)^2+4>=4\forall x\)
=>\(B=\dfrac{20}{\left(2x-1\right)^2+4}< =\dfrac{20}{4}=5\forall x\)
Dấu '=' xảy ra khi 2x-1=0
=>\(x=\dfrac{1}{2}\)
b: \(x^2+1>=1\forall x\)
=>\(\left(x^2+1\right)^2>=1^2=1\forall x\)
=>\(\left(x^2+1\right)^2+5>=1+5=6\forall x\)
=>\(C=\dfrac{10}{\left(x^2+1\right)^2+5}< =\dfrac{10}{6}=\dfrac{5}{3}\forall x\)
Dấu '=' xảy ra khi x=0