Cần gấp 3 bài này ạ. Mình cảm ơn....
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.





\(x=\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\)
\(\Rightarrow x^3=9+4\sqrt{5}+9-4\sqrt{5}+3\sqrt[3]{\left(9+4\sqrt[]{5}\right)\left(9-4\sqrt{5}\right)}\left(\sqrt[3]{9+4\sqrt{5}}+\sqrt[3]{9-4\sqrt{5}}\right)\)
\(=18+3\sqrt{81-80}.x=18+3x\)\(\Rightarrow x^3-3x=18\left(1\right)\)
\(y=\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\)
\(\Rightarrow y^3=3+2\sqrt{2}+3-2\sqrt{2}+3\sqrt[3]{\left(3+2\sqrt{2}\right)\left(3-2\sqrt{2}\right)}\left(\sqrt[3]{3+2\sqrt{2}}+\sqrt[3]{3-2\sqrt{2}}\right)\)
\(=6+3\sqrt[3]{9-8}.y=6+3y\)\(\Rightarrow y^3-3y=6\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow P=x^3+y^3-3\left(x+y\right)+1996=x^3-3x+y^3-3y+1996\)
\(=18+6+1996=2020\)

2:
a: =(1+căn 3)^2-5
=4+2căn 3-5
=2căn 3-1
b: \(=\sqrt{\dfrac{125}{7}\cdot\dfrac{35}{81}}=\sqrt{\dfrac{625}{81}}=\dfrac{25}{9}\)
c: \(=\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)-\sqrt{6}+\sqrt{2}\)
=2-căn 6+căn 2
3:
a: \(=\dfrac{2\sqrt{3}+3\sqrt{3}-\sqrt{3}}{\sqrt{3}}=2+3-1=5\)
b: \(=\dfrac{6\sqrt{2}+7\sqrt{2}-5\sqrt{2}}{\sqrt{2}}=13-5=8\)
c: \(=\dfrac{12-10+8}{2}=5\)
d: \(=\sqrt{\dfrac{1}{5}:5}-\sqrt{\dfrac{9}{5}:5}+\sqrt{5:5}\)
=1/5-3/5+1
=3/5










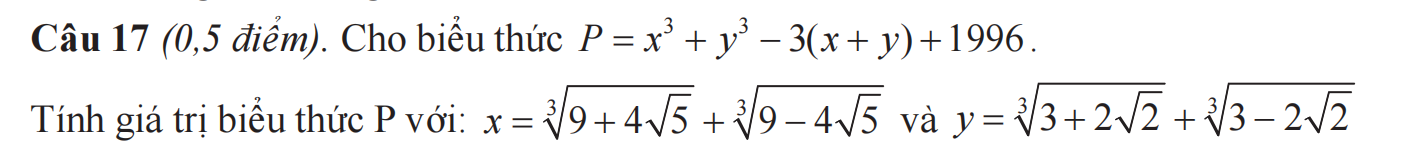 cảm ơn
cảm ơn 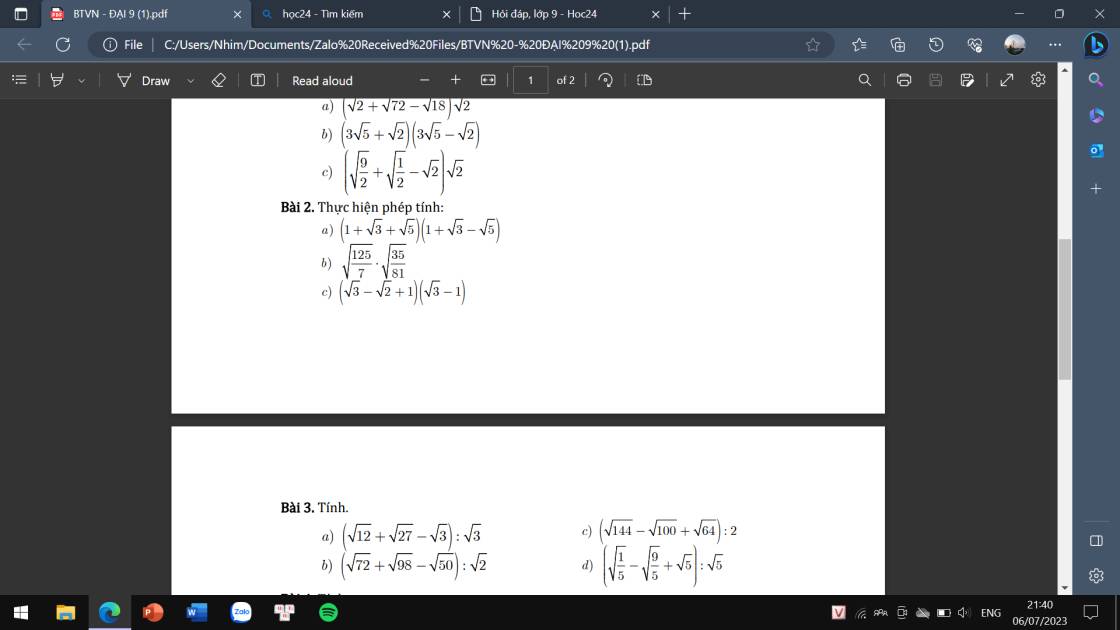



17:
a: Gọi hai số tự nhiên liên tiếp là a;a+1
Hiệu bình phương của chúng là 209 nên ta có:
\(\left(a+1\right)^2-a^2=209\)
=>\(a^2+2a+1-a^2=209\)
=>2a+1=209
=>2a=208
=>a=104
vậy: Hai số cần tìm là 104;104+1=105
b: Gọi hai số tự nhiên lẻ liên tiếp là 2k+1;2k+3
Hiệu lập phương của chúng là 1178 nên ta có:
\(\left(2k+3\right)^3-\left(2k+1\right)^3=1178\)
=>\(8k^3+36k^2+54k+27-8k^3-12k^2-6k-1=1178\)
=>\(24k^2+48k+26-1178=0\)
=>\(24k^2+48k-1152=0\)
=>\(\left[{}\begin{matrix}k=6\left(nhận\right)\\k=-8\left(loại\right)\end{matrix}\right.\)
Vậy: Hai số cần tìm là \(2\cdot6+1=13;2\cdot6+3=15\)
19:
a: \(A=x^2-4x+10\)
\(=x^2-4x+4+6\)
\(=\left(x-2\right)^2+6>=6>0\forall x\)
=>ĐPCM
b: \(B=2x^2-2x+3\)
\(=2\left(x^2-x+\dfrac{3}{2}\right)\)
\(=2\left(x^2-x+\dfrac{1}{4}+\dfrac{5}{4}\right)\)
\(=2\left(x-\dfrac{1}{2}\right)^2+\dfrac{5}{2}>=\dfrac{5}{2}>0\forall x\)
=>ĐPCM
c: \(C=x^4-3x^2+5\)
\(=x^4-3x^2+\dfrac{9}{4}+\dfrac{11}{4}\)
\(=\left(x^2-\dfrac{3}{2}\right)^2+\dfrac{11}{4}>=\dfrac{11}{4}>0\forall x\)
=>ĐPCM
d: \(D=\dfrac{1}{4}x^4+\dfrac{2}{5}x^2+2\)
\(=x^2\left(\dfrac{1}{4}x^2+\dfrac{2}{5}\right)+2>=2>0\forall x\)
=>ĐPCM
e: \(E=x^2+\left(x+1\right)^2\)
\(=x^2+x^2+2x+1=2x^2+2x+1\)
\(=2\left(x^2+x+\dfrac{1}{2}\right)=2\left(x^2+x+\dfrac{1}{4}+\dfrac{1}{4}\right)\)
\(=2\left(x+\dfrac{1}{2}\right)^2+\dfrac{1}{2}>=\dfrac{1}{2}>0\forall x\)
=>ĐPCM
f: \(F=\left(x-2\right)^2+\left(x-4\right)^2\)
\(=x^2-4x+4+x^2-8x+16\)
\(=2x^2-12x+20=2\left(x^2-6x+10\right)\)
\(=2\left(x^2-6x+9+1\right)=2\left[\left(x-3\right)^2+1\right]>=2\cdot1=2>0\forall x\)
g: \(G=x^2+y^2+2x-6y+11\)
\(=x^2+2x+1+y^2-6y+9+1\)
\(=\left(x+1\right)^2+\left(y-3\right)^2+1>=1>0\forall x,y\)
=>ĐPCM