Cho tam giác ABC có AM là đường trung tuyến, N là điểm trên đoạn thẳng AM . Gọi D là giao điểm của CN và AB , E là giao điểm của BN và AC . Chọn khẳng định đúng nhất. A. DE/ /BC B. AD/BD=AE/ CE . C. Cả A, B đều đúng. D. Cả A, B đều sai.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
13 tháng 11 2018
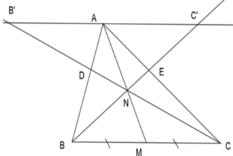
Kẻ đường thẳng đi qua A song song với BC lần lượt cắt CD và BE kéo dài tại B’ và C’.
Vì M là trung điểm BC nên BM = MC.
Vì AB’ // MC, áp dụng định lý Talet ta có: A N N M = A B ' M C (1)
Vì AC’ // BM, áp dụng định lý Talet ta có: A N N M = A C ' M B (2)
Từ (1) và (2) ta có: A B ' M C = A C ' B M
Ta có M là trung điểm BC => BM = MC => AB’ = AC’ (*)
Vì AB’ // BC, áp dụng định lý Talet ta có: A D D B = A B ' B C (**)
Vì AC’ // BC, áp dụng định lý Talet ta có: A E E C = A C ' B C (***)
Từ (*), (**) và (***) ta có:
A D D B = A B ' B C = A E E C = A C ' B C ⇒ A D D B = A E E C ⇔ A D B D = A E C E
hay DE // BC
Đáp án: C
SK
10 tháng 3 2020
a, Ta có:
góc DAB = góc EAC( Vì cùng phụ góc BAC)
AD= AC
AB=AE
Nên tam giác ABD = tam giác AEC
Vây BD = CEb,
Ta có: ACNB là hình bình hành nên góc ACN + góc BAC = 180độ (1)
Mặt khác ta có : 2( góc DAB +góc BAC) = 2. 90 độ = 180độ
Nên góc DAB + góc EAC + góc BAC + góc BAC = 180 độ
Suy ra DAE + BAC = 180 độ (2)
Từ (1) và (2) ta đc góc DAE = góc ACN
Mà AD = AC; AB= CN nên tam giác ADE = Tam giác cân
c, Ta có: góc NAC = góc ADE ( cmt )
Mà góc NAC + góc DAM = 90 độ nên ADE + góc DAM = 90 độ
Vậy DIA = 90 độ
Áp dụng pytago ta có:\(\frac{AD^2+IE^2}{DI^2+AE^2}=\frac{\left(AD^2+DI^2\right)+\left(AE^2-AI^2\right)}{DI^2+AE^2}=1\)
21 tháng 6 2022
Câu 3:
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD
Kéo dài CD, BE sao cho chúng cắt đường thẳng song song với BC đi qua A lần lượt tại K, G.
Xét \(\Delta NMC\) có: \(AK//MC\text{ (}AK//BC;M\in BC)\)
\(\Rightarrow\dfrac{AN}{NM}=\dfrac{AK}{MC}\) (hệ quả đli Talet) (1)
Xét \(\Delta NMB\) có: \(AG//MB\text{ (}AG//BC;M\in BC)\)
\(\Rightarrow\dfrac{AN}{NM}=\dfrac{AG}{MB}\) (hệ quả đli Talet) (2)
Từ (1) và (2) \(\Rightarrow\dfrac{AK}{MC}=\dfrac{AG}{MB}\)
Mà \(MB=MC\) (vì M là trung điểm BC) nên \(AK=AG\) (3)
Xét \(\Delta BDC\) có: \(AK//BC\Rightarrow \dfrac{AD}{BD}=\dfrac{AK}{BC}\) (hệ quả đli Talet) (4)
Xét \(\Delta CEB\) có: \(AG//BC\Rightarrow \dfrac{AE}{EC}=\dfrac{AG}{BC}\) (hệ quả đli Talet) (5)
Từ (3), (4) và (5) \(\Rightarrow\dfrac{AD}{BD}=\dfrac{AE}{EC}\Rightarrow\dfrac{AD}{AD+BD}=\dfrac{AE}{AE+EC}\)
\(\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Xét \(\Delta ABC\) có: \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\) (cmt) \(\Rightarrow DE//BC\) (đli Talet đảo)
\(\rightarrow\) Chọn C. Cả A và B đều đúng
$Toru$