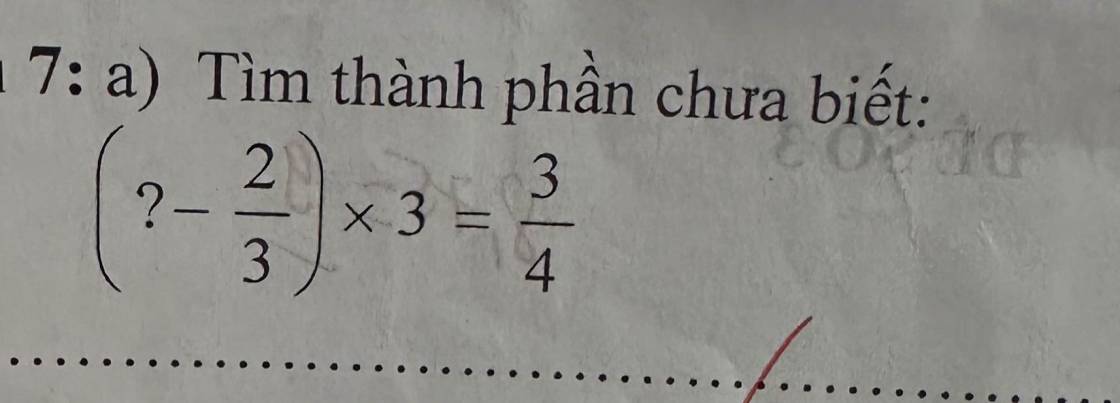 Cả nhà giúp em với ạ
Cả nhà giúp em với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


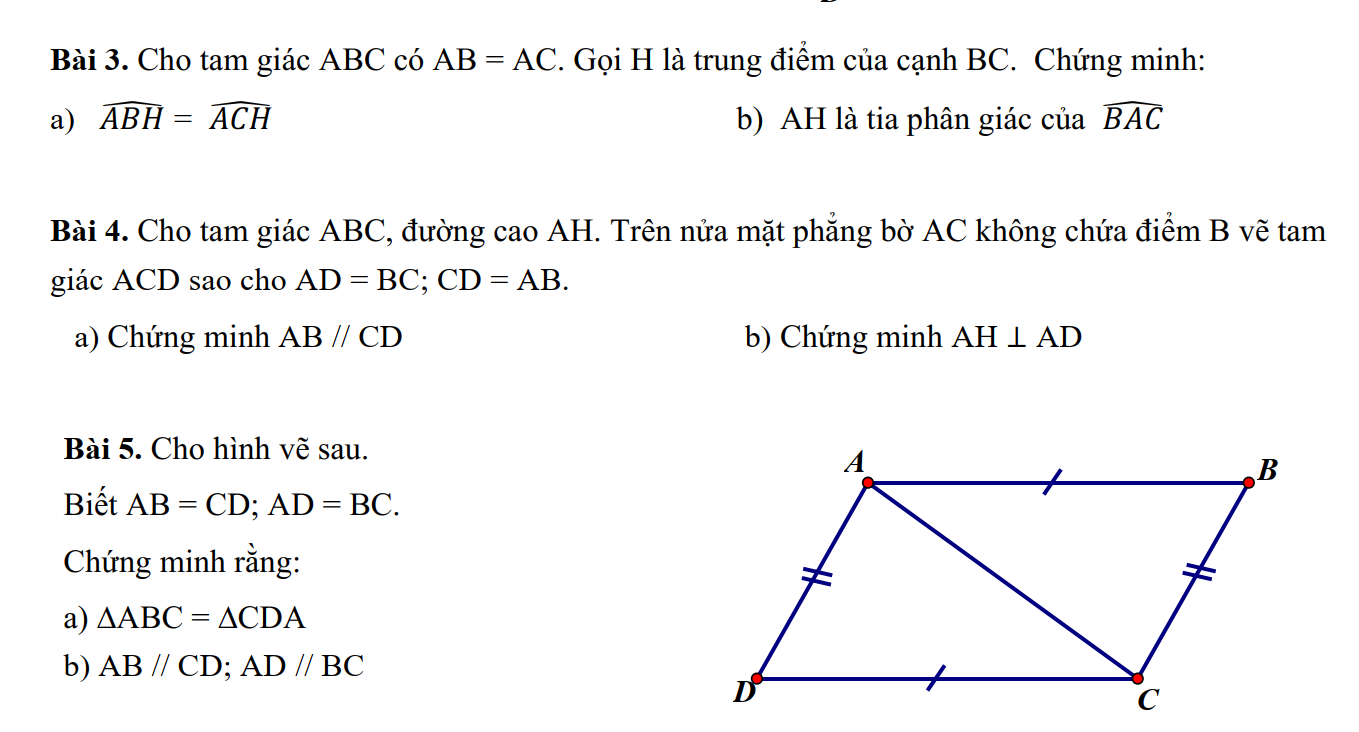
\(5,\\ a,\left\{{}\begin{matrix}AB=CD\left(gt\right)\\AD=BC\left(gt\right)\\AC.chung\end{matrix}\right.\Rightarrow\Delta ABC=\Delta CDA\left(c.c.c\right)\\ b,\Delta ABC=\Delta CDA\left(cm.trên\right)\\ \Rightarrow\left\{{}\begin{matrix}\widehat{CAB}=\widehat{DCA}\\\widehat{CAD}=\widehat{ACB}\end{matrix}\right.\left(các.cặp.góc.tương.ứng\right)\)
Mà các cặp góc này ở vị trí so le trong nên \(AB//CD;AD//BC\)



Cả nhà giúp em với ạ!Em biết nghỉ hè sẽ không ai lên online math đâu nhưng em vẫn tin có vài người vẫn đang lên mà!Mọi người giúp em đi ạ

có thể viết được : 4670,4760,6740,6470,7460,7640,4706,4607,6704,

Bài 5:
a. Tiền lãi là \(100000000.0,6\%=600000\left(đồng\right)\)
Tổng tiền là \(100000000+600000=100600000\left(đồng\right)\)
b. Sau 2 tháng tổng tiền là \(100600000+600000=101200000\left(đồng\right)\)

Vào mùng 10 tháng Giêng hàng năm, người dân Bắc Ninh quê em lại náo nức tổ chức hội Lim- Lễ hội truyền thống của địa phương em. Vào ngày hội, mọi người đều diện lên mình những bộ trang phục đẹp để đi hội. Hội Lim có rất nhiều trò chơi dân gian thú vị như: Kéo co, chọi gà, đấu cờ, đấu vật. Một hoạt động văn hóa khác được tổ chức ở hội Lim được đông đảo mọi người yêu thích, đó là hát quan họ. Tại bờ sông, các liền anh, liền chị hát đối đáp trên thuyền thu hút đông đảo khán giả thưởng thức. Trong những ngày tổ chức lễ hội, không chỉ có người dân ở địa phương em mà còn rất nhiều du khách từ những địa phương khác cũng về đây trẩy hội. Hội Lim là một ngày hội truyền thống, một nét đẹp văn hóa mà bất cứ người nào sinh sống trên quê hương Bắc Ninh đều cảm thấy yêu thích và tự hào.

Lời giải:
\(f(x)=\sin x\Rightarrow f'(x)=\cos x; g(x)=\cot x\Rightarrow g'(x)=-\frac{1}{\sin ^2x}\)
\(\Rightarrow \frac{f'(\frac{\pi}{4})}{g'(\frac{\pi}{4})}=-\cos (\frac{\pi}{4})\sin ^2(\frac{\pi}{4})=\frac{-\sqrt{2}}{4}\)

a: \(N\in SB\subset\left(SBC\right)\)
\(N\in\left(NAD\right)\)
Do đó: \(N\in\left(SBC\right)\cap\left(NAD\right)\)
Xét (SBC) và (NAD) có
\(N\in\left(SBC\right)\cap\left(NAD\right)\)
BC//AD
Do đó: (SBC) giao (NAD)=xy, xy đi qua N và xy//BC//AD
b: Trong mp(ABCD), Gọi O là giao điểm của AC và BD
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\left(1\right)\)
\(S\in SA\subset\left(SAC\right)\)
\(S\in SB\subset\left(SBD\right)\)
Do đó: \(S\in\left(SAC\right)\cap\left(SBD\right)\left(2\right)\)
Từ (1) và (2) suy ra (SAC) giao (SBD)=SO
c: Chọn mp(SBC) có chứa NK
\(SC\subset\left(SBC\right)\)
\(SC\subset\left(SCA\right)\)
Do đó: \(\left(SBC\right)\cap\left(SCA\right)=SC\)
Gọi E là giao điểm của NK với SC
=>E là giao điểm của NK với mp(SAC)
d: Chọn mp(SBD) có chứa DN
Ta có: (SBD) giao (SAC)=SO(cmt)
nên ta sẽ gọi F là giao điểm của SO với DN
=>F là giao điểm của ND với mp(SAC)
e: Xét ΔSAB có
M,N lần lượt là trung điểm của SA,SB
=>MN là đường trung bình của ΔSAB
=>MN//AB và \(MN=\dfrac{AB}{2}\)
MN//AB
AB//CD
Do đó: MN//CD
Xét tứ giác MNCD có MN//CD
nên MNCD là hình thang

 cả nhà giúp mk với ạ,em cần gấp!
cả nhà giúp mk với ạ,em cần gấp!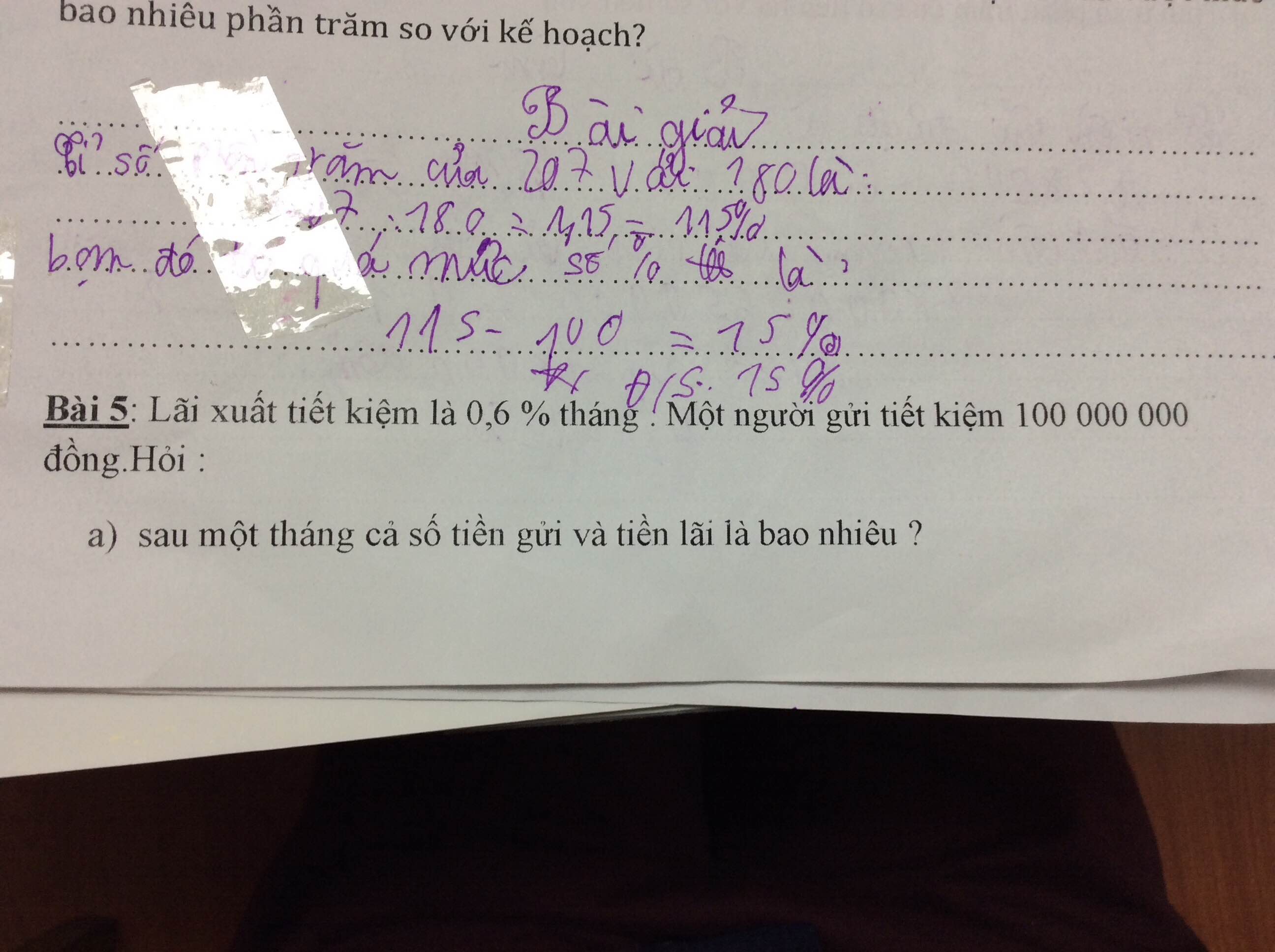
 Cả nhà giúp với ạ!
Cả nhà giúp với ạ!

(? - \(\dfrac{2}{3}\)) x 3 = \(\dfrac{3}{4}\)
(? - \(\dfrac{2}{3}\)) = \(\dfrac{3}{4}\) : 3
? - \(\dfrac{2}{3}\) = \(\dfrac{1}{4}\)
? = \(\dfrac{1}{4}\) + \(\dfrac{2}{3}\)
? = \(\dfrac{11}{12}\)