 giúp em bài 12 13 với ạ
giúp em bài 12 13 với ạ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


11.
\(=\frac{\sqrt{x}-3}{2-\sqrt{x}}+\frac{\sqrt{x}-2}{3+\sqrt{x}}+\frac{9-x}{(2-\sqrt{x})(\sqrt{x}+3)}\)
\(=\frac{(\sqrt{x}-3)(\sqrt{x}+3)}{(2-\sqrt{x})(\sqrt{x}+3)}+\frac{\sqrt{x}-2}{3+\sqrt{x}}+\frac{9-x}{(2-\sqrt{x})(\sqrt{x}+3)}\)
\(=\frac{x-9}{(2-\sqrt{x})(\sqrt{x}+3)}+\frac{\sqrt{x}-2}{3+\sqrt{x}}+\frac{9-x}{(2-\sqrt{x})(\sqrt{x}+3)}\)
\(=\frac{\sqrt{x}-2}{3+\sqrt{x}}\)
12.
\(=\frac{(3-\sqrt{x})(3\sqrt{x}-2)+(5\sqrt{x}+7)(3\sqrt{x}+4)}{(5\sqrt{x}+7)(3\sqrt{x}-2)}-\frac{42\sqrt{x}+34}{(5\sqrt{x}+7)(3\sqrt{x}-2)}\)
\(=\frac{12x+52\sqrt{x}+22}{(5\sqrt{x}+7)(3\sqrt{x}-2)}-\frac{42\sqrt{x}+34}{(5\sqrt{x}+7)(3\sqrt{x}-2)}\)
\(=\frac{12x+10\sqrt{x}-12}{(5\sqrt{x}+7)(3\sqrt{x}-2)}=\frac{2(3\sqrt{x}-2)(2\sqrt{x}+3)}{(5\sqrt{x}+7)(3\sqrt{x}-2)}=\frac{2(2\sqrt{x}+3)}{5\sqrt{x}+7}\)

Bài 13:
góc A=180-80-30=70 độ
=>góc BAD=góc CAD=70/2=35 độ
góc ADC=80+35=115 độ
góc ADB=180-115=65 độ
Bài 14:
Xét ΔABC vuông tại A
-> \(\widehat{B}\)\(+ \widehat{C}=90^o\)
Mà \(\widehat{B}=\widehat{C}\)
=> \(2\widehat{B}=90^o\)
=> \(\widehat{B}=45^o\)


14.
\(\dfrac{1-cosa}{sina}=\dfrac{sina\left(1-cosa\right)}{sin^2a}=\dfrac{sina\left(1-cosa\right)}{1-cos^2a}=\dfrac{sin\left(1-cosa\right)}{\left(1-cosa\right)\left(1+cosa\right)}=\dfrac{sina}{1+cosa}\)
Câu b đề bài sai, đẳng thức đúng phải là: \(1+tan^2a=\dfrac{1}{cos^2a}\)
\(1+tan^2a=1+\dfrac{sin^2a}{cos^2a}=\dfrac{sin^2a+cos^2a}{cos^2a}=\dfrac{1}{cos^2a}\)
\(tan^2a-sin^2a=\dfrac{sin^2a}{cos^2a}-sin^2a=\dfrac{sin^2a}{cos^2a}\left(1-cos^2a\right)=\dfrac{sin^2a}{cos^2a}.sin^2a=tan^2a.sin^2a\)
\(\dfrac{sin^4a-cos^4a}{sina+cosa}=\dfrac{\left(sin^2a+cos^2a\right)\left(sin^2a-cos^2a\right)}{sina+cosa}=\dfrac{sin^2a-cos^2a}{sina+cosa}=\dfrac{\left(sina+cosa\right)\left(sina-cosa\right)}{sina+cosa}\)
\(=sina-cosa\)
13.
b. Chia cả tử và mẫu cho sinB:
\(N=\dfrac{\dfrac{4cosB}{sinB}+\dfrac{2sinB}{sinB}}{\dfrac{cossB}{sinB}-\dfrac{3sinB}{sinB}}=\dfrac{4cotB+2}{cotB-3}=\dfrac{4.\dfrac{3}{2}+2}{\dfrac{3}{2}-3}=-\dfrac{16}{3}\)
c. Chia cả tử và mẫu cho \(cos^3B\)
\(M=\dfrac{\dfrac{sin^3B}{cos^3B}-\dfrac{cos^3B}{cos^3B}}{\dfrac{sin^3B}{cos^3B}+\dfrac{cos^3B}{cos^3B}}=\dfrac{tan^3B-1}{tan^3B+1}=\dfrac{3^3-1}{3^3+1}=\dfrac{13}{14}\)

Bài 11:
Gọi số học sinh giỏi 4 khối lần lượt là $a,b,c,d$ (em)
Theo bài ra ta có: $a+b+c-d=168$ và $\frac{a}{13}=\frac{b}{12}=\frac{c}{14}=\frac{d}{15}$
Áp dụng tính chất dãy tỉ số bằng nhau:
$\frac{a}{13}=\frac{b}{12}=\frac{c}{14}=\frac{d}{15}=\frac{a+b+c-d}{13+12+14-15}=\frac{168}{24}=7$
$\Rightarrow a=13.7=91; b=12.7=84; c=14.7=98; d=15.7=105$
Bài 12:
Gọi số học sinh ba khối lần lượt là $a,b,c$ (học sinh).
Theo bài ra ta có: $\frac{a}{10}=\frac{b}{9}=\frac{c}{8}$ và $a-b=50$
Áp dụng TCDTSBN:
$\frac{a}{10}=\frac{b}{9}=\frac{c}{8}=\frac{a-b}{10-9}=\frac{50}{1}=50$
$\Rightarrow a=50.10=500; b=50.9=450; c=50.8=400$ (hs)

\(\dfrac{7}{12}=\dfrac{3}{12}+\dfrac{4}{12}=\dfrac{1}{4}+\dfrac{1}{3}\)
\(\dfrac{13}{27}=\dfrac{9}{27}+\dfrac{4}{27}=\dfrac{1}{3}+\dfrac{4}{27}\)
\(\dfrac{7}{12}\) = \(\dfrac{1+6}{12}\) = \(\dfrac{1}{12}\) + \(\dfrac{6}{12}\) = \(\dfrac{1}{12}\) + \(\dfrac{1}{2}\)
\(\dfrac{7}{12}\) = \(\dfrac{3+4}{12}\) = \(\dfrac{3}{12}\) + \(\dfrac{4}{12}\) = \(\dfrac{1}{4}\) + \(\dfrac{1}{3}\)
\(\dfrac{13}{27}\) = \(\dfrac{1+12}{27}\) = \(\dfrac{1}{27}\) + \(\dfrac{12}{27}\) = \(\dfrac{1}{27}\) + \(\dfrac{4}{9}\)
\(\dfrac{13}{27}\) = \(\dfrac{4+9}{27}\) = \(\dfrac{4}{27}\) + \(\dfrac{9}{27}\) = \(\dfrac{4}{27}\) + \(\dfrac{1}{3}\)
\(\dfrac{13}{27}\) = \(\dfrac{6+7}{27}\) = \(\dfrac{6}{27}\) + \(\dfrac{7}{27}\) = \(\dfrac{2}{9}\) + \(\dfrac{7}{27}\)

13:
\(=\dfrac{1}{sin\left(\dfrac{pi}{33}\right)}sin\left(\dfrac{pi}{33}\right)\cdot cos\left(\dfrac{pi}{33}\right)\cdot cos\left(\dfrac{2pi}{33}\right)\cdot cos\left(\dfrac{4pi}{33}\right)\cdot cos\left(\dfrac{8pi}{33}\right)\cdot cos\left(\dfrac{16pi}{33}\right)\)
\(=\dfrac{1}{sin\left(\dfrac{pi}{33}\right)}\cdot\dfrac{1}{2}\cdot sin\dfrac{2}{33}pi\cdot cos\left(\dfrac{2}{33}pi\right)cos\left(\dfrac{4}{33}pi\right)\cdot cos\left(\dfrac{8}{33}pi\right)\cdot cos\left(\dfrac{16}{33}pi\right)\)
\(=\dfrac{1}{sin\left(\dfrac{pi}{33}\right)}\cdot\dfrac{1}{2}\cdot sin\dfrac{2}{33}pi\cdot cos\left(\dfrac{2}{33}pi\right)cos\left(\dfrac{4}{33}pi\right)\cdot cos\left(\dfrac{8}{33}pi\right)\cdot cos\left(\dfrac{16}{33}pi\right)\)\(=\dfrac{1}{sin\left(\dfrac{pi}{33}\right)}\cdot\dfrac{1}{4}\cdot sin\dfrac{4}{33}pi\cdot cos\left(\dfrac{4}{33}pi\right)\cdot cos\left(\dfrac{8}{33}pi\right)\cdot cos\left(\dfrac{16}{33}pi\right)\)
\(=\dfrac{1}{sin\left(\dfrac{pi}{33}\right)}\cdot\dfrac{1}{8}\cdot sin\dfrac{8}{33}pi\cdot cos\left(\dfrac{8}{33}pi\right)\cdot cos\left(\dfrac{16}{33}pi\right)\)
\(=\dfrac{1}{sin\left(\dfrac{pi}{33}\right)}\cdot\dfrac{1}{16}\cdot sin\dfrac{16}{33}pi\cdot cos\left(\dfrac{16}{33}pi\right)\)
\(=\dfrac{1}{sin\left(\dfrac{pi}{3}\right)}\cdot\dfrac{1}{32}\cdot sin\dfrac{32}{33}pi\)
=1/32
10:
\(=\dfrac{1}{2}\left[cos100+cos60\right]+\dfrac{1}{2}\cdot\left[cos100+cos20\right]\)
=cos100+1/2*cos20+1/4
6:
sin6*cos12*cos24*cos48
=1/cos6*cos6*sin6*cos12*cos24*cos48
=1/cos6*1/2*sin12*cos12*cos24*cos48
=1/cos6*1/4*sin24*cos24*cos48
=1/cos6*1/8*sin48*cos48
=1/cos6*1/16*sin96
=1/16

 giải giúp em bài 11 12 13 của bài 14 đi ạ
giải giúp em bài 11 12 13 của bài 14 đi ạ


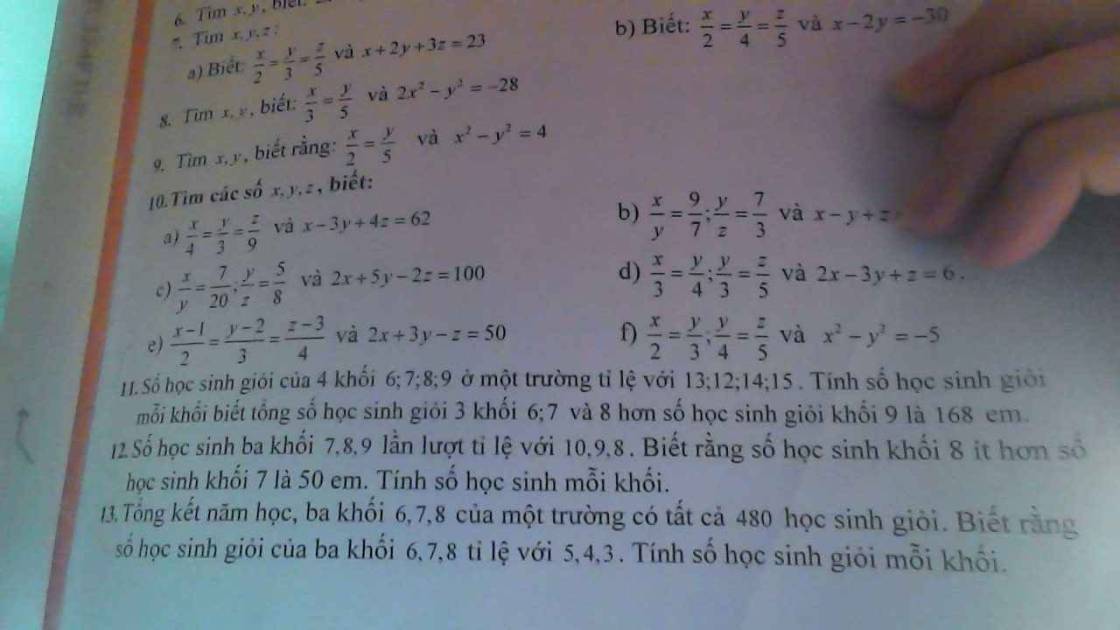


Bài 12:
a: (d): \(\left\{{}\begin{matrix}x=-2-2t\\y=1+2t\end{matrix}\right.\)
=>(d) đi qua T(-2;1) và có vecto chỉ phương là (-2;2)
(d')\(\perp\)(d) nên (d') nhận vecto (-2;2) làm vecto pháp tuyến
Phương trình (d') là:
-2(x-3)+2(y-1)=0
=>-(x-3)+(y-1)=0
=>-x+3+y-1=0
=>-x+y+2=0
b: (d) có vecto chỉ phương là (-2;2)
=>(d) có vecto pháp tuyến là (2;2)=(1;1)
Phương trình (d) là:
1(x+2)+1(y-1)=0
=>x+2+y-1=0
=>x+y+1=0
Tọa độ giao điểm H của (d) và (d') là:
\(\left\{{}\begin{matrix}x+y+1=0\\-x+y+2=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x+y=-1\\-x+y=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=-3\\x+y=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-\dfrac{3}{2}\\y=-1-x=-1+\dfrac{3}{2}=\dfrac{1}{2}\end{matrix}\right.\)
c: A' đối xứng với A qua d
=>A'A\(\perp\)d
mà d'\(\perp\)d và \(A\in d'\)
nên d' chính là phương trình AA'
=>H là trung điểm của A'A
A(3;1); H(-3/2;1/2); A'(x;y)
H là trung điểm của A'A
=>\(\left\{{}\begin{matrix}x_A+x_{A'}=2\cdot x_H=-3\\y_A+y_{A'}=2\cdot y_H=2\cdot\dfrac{1}{2}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x_{A'}+3=-3\\y_A+1=1\end{matrix}\right.\)
=>A'(-6;0)
Bài 13:
a: M(2;-5); N(4;-3)
Tọa độ tâm I là:
\(\left\{{}\begin{matrix}x=\dfrac{2+4}{2}=\dfrac{6}{2}=3\\y=\dfrac{-5+\left(-3\right)}{2}=-\dfrac{8}{2}=-4\end{matrix}\right.\)
I(3;-4); M(2;-5)
\(IM=\sqrt{\left(2-3\right)^2+\left(-5+4\right)^2}=\sqrt{2}\)
Phương trình (C) là:
\(\left(x-3\right)^2+\left(y+4\right)^2=IM^2=2\)
b: (C) có tâm là I(1;-2) và tiếp xúc với đường thẳng 4x-3y+5=0
=>Bán kính là \(R=d\left(I;4x-3y+5=0\right)=\dfrac{\left|1\cdot4+\left(-2\right)\cdot\left(-3\right)+5\right|}{\sqrt{4^2+\left(-3\right)^2}}=\dfrac{15}{5}=3\)
Phương trình (C) là:
\(\left(x-1\right)^2+\left(y+2\right)^2=R^2=9\)
c: Gọi phương trình (C) là: \(x^2+y^2+2ax+2by+c=0\)
Thay x=1 và y=0 vào (C), ta được:
\(1^2+0^2+2\cdot a\cdot1+2\cdot b\cdot0+c=0\)
=>2a+c=-1(1)
Thay x=0 và y=-2 vào (C), ta được:
\(0^2+\left(-2\right)^2+2\cdot a\cdot0+2\cdot b\cdot\left(-2\right)+c=0\)
=>4-4b+c=0
=>-4b+c=-4(2)
Thay x=2 và y=3 vào (C), ta được:
\(2^2+3^2+2\cdot a\cdot2+2\cdot b\cdot3+c=0\)
=>4a+6b+c=-13(3)
Từ (1),(2),(3) ta có hệ phương trình:
\(\left\{{}\begin{matrix}2a+c=-1\\-4b+c=-4\\4a+6b+c=-13\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2a+4b=-1+4=5\\-2a-6b=-1+13=12\\2a+c=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2b=5+12=17\\2a+4b=5\\2a+c=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=-\dfrac{17}{2}\\2a=5-4b=5-4\cdot\dfrac{-17}{2}=5+34=39\\2a+c=-1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=-\dfrac{17}{2}\\a=\dfrac{39}{2}\\c=-1-2a=-1-2\cdot\dfrac{39}{2}=-40\end{matrix}\right.\)
Vậy: (C): \(x^2+y^2+39x-17y-40=0\)