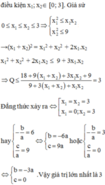xét phương trình bậc hai ax²+bx+c=0 có hai nghiệm thuộc [0, 2]. tìm giá trị lớn nhất của biểu thức P=(8a²-6ab+b²)/(4a²-2ab+ac)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 7 2018
Theo Vi- ét ta có: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}\\x_1.x_2=\dfrac{c}{a}\end{matrix}\right.\)
Suy ra: P = \(\dfrac{8+6\left(x_1+x_2\right)+\left(x_1+x_2\right)^2}{4+2\left(x_1+x_2\right)+x_1x_2}\)
Giả sử 0 \(\le x_1\le x_2\le2\) ta có: \(x_1^2\le x_1x_2\); x22 \(\le4\)
Do đó: \(x_1^2+x_2^2\le x_1x_2+4\) suy ra \(x_1^2+x^2_2+2x_1x_2\le4+3x_1x_2\)
hay \(\left(x_1+x_2\right)^2\le4+3x_1x_2\)
Suy ra P \(\le\dfrac{8+6\left(x_1+x_2\right)+4+3x_1x_2}{4+2\left(x_1+x_2\right)+x_1x_2}\) = 3
HQ
Hà Quang Minh
Giáo viên
24 tháng 9 2023
Mệnh đề \(P \Rightarrow Q\): “Nếu phương trình bậc hai \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt thì phương trình bậc hai \(a{x^2} + bx + c = 0\) có biệt thức \(\Delta = {b^2} - 4ac\;\, > 0\).”
Mệnh đề \(Q \Rightarrow P\): “Nếu phương trình bậc hai \(a{x^2} + bx + c = 0\) có biệt thức \(\Delta = {b^2} - 4ac\;\, > 0\) thì phương trình bậc hai \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt.”
24 tháng 10 2021
Bài 3:
#include <bits/stdc++.h>
using namespace std;
double a,b,c,delta,x1,x2;
int main()
{
//freopen("PTB2.inp","r",stdin);
//freopen("PTB2.out","w",stdout);
cin>>a>>b>>c;
delta=(b*b-4*a*c);
if (delta<0) cout<<"-1";
if (delta==0) cout<<fixed<<setprecision(5)<<(-b/(2*a));
if (delta>0)
{
x1=(-b-sqrt(delta))/(2*a);
x2=(-b+sqrt(delta))/(2*a);
cout<<fixed<<setprecision(5)<<x1<<" "<<fixed<<setprecision(5)<<x2;
}
return 0;
}
24 tháng 10 2021
4 bước : xác định bài toán , ý tưởng , thuật toán , mô phỏng làm như nào ạ ?