Cho tam giác ABC vuông tại A.Tia phân giác của góc ABC cắt cạnh AC tại D.Kẻ DE vuông góc với BC (E thuộc BC)
a)Chưng minh tam giác ABD= tam giác EBD từ đó so sánh DA và DC
b)Gọi K là gioa điểm của BA và ED.Đường thẳng BD cắt CK tại H.Chứng minh tam giác KDC cân và BH vuông góc với KC




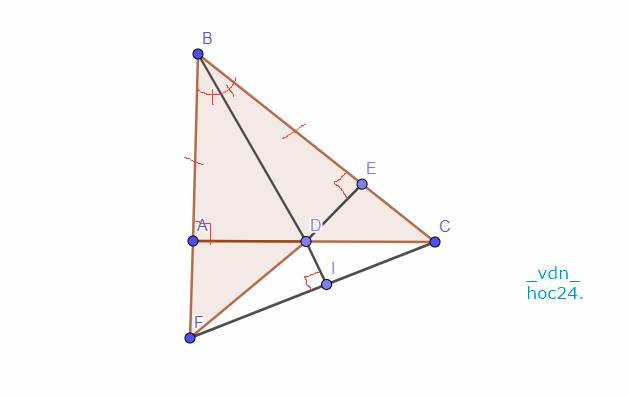
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
=>DA=DE
mà DE<DC(ΔDEC vuông tại E)
nên DA<DC
b: Xét ΔDAK vuông tại A và ΔDEC vuông tại E có
DA=DE
\(\widehat{ADK}=\widehat{EDC}\)(hai góc đối đỉnh)
Do đó: ΔDAK=ΔDEC
=>DK=DC
=>ΔDKC cân tại D
Xét ΔBKC có
KE,CA là các đường cao
KE cắt CA tại D
Do đó: D là trực tâm của ΔBKC
=>BD\(\perp\)KC tại H