Qua B kẻ đường thẳng vuông góc với BE cắt FD tại G chứng minh BG song song với FC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn tự vẽ hình nha![]()
a.
Xét tam giác ABI và tam giác EBI có:
AIB = EIB ( = 900)
BI là cạnh chung
IBA = IBE (BI là tia phân giác của ABE)
=> Tam giác ABI = Tam giác EBI (g.c.g)
=> AB = EB (2 cạnh tương ứng)
b.
Xét tam giác ABD và tam giác EBD có:
BA = BE (theo câu a)
ABD = EBD (BD là tia phân giác của ABE)
BD là cạnh chung
=> Tam giác ABD = Tam giác EBD (c.g.c)
=> BAD = BED (2 góc tương ứng)
mà BAD = 900
=> BED = 900
=> Tam giác BED vuông tại E
c.
BA = BE (theo câu a)
=> Tam giác BAE cân tại B
=> \(BAE=\frac{180^0-ABE}{2}\) (1)
Xét tam giác ADF và tam giác EDC có:
ADF = EDC (2 góc đối đỉnh)
AD = ED (tam giác ABD = tam giác EBD)
FAD = CED ( = 900)
=> Tam giác ADF = Tam giác EDC (g.c.g)
Ta có:
BF = BA + AF
BC = BE + EC
mà BA = BE (theo câu a)
AF = EC (tam giác ADF = tam giác EDC)
=> BF = BC
=> Tam giác BFC cân tại B
=> \(BFC=\frac{180^0-FBC}{2}\) (2)
Từ (1) và (2)
=> BAE = BFC
mà 2 góc này ở vị trí đồng vị
=> AE // FC
Chúc bạn học tốt![]()

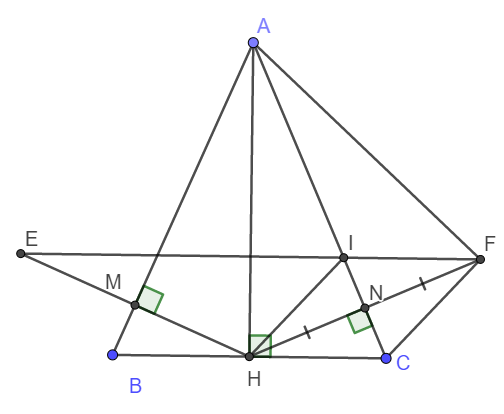
a) Do ABC là tam giác cân tại A nên AH là đường cao hay đồng thời là đường phân giác.
Xét tam giác vuông AMH và tam giác vuông ANH có:
Cạnh AH chung
\(\widehat{MAH}=\widehat{NAH}\)
\(\Rightarrow\Delta AMH=\Delta ANH\) (Cạnh huyền - góc nhọn)
\(\Rightarrow HM=HN.\)
b) Dễ dàng thấy ngay AC là đường trung trực của HF.
Khi đó thì AH = AF; CH = CF
Xét tam giác AHC và tam giác AFC có:
Cạnh AC chung
AH - AF
CH = CF
\(\Rightarrow\Delta AHC=\Delta AFC\left(c-c-c\right)\)
\(\Rightarrow\widehat{AFC}=\widehat{AHC}=90^o\Rightarrow AF\perp CF.\)
c) Ta thấy ngay \(\Delta HIN=\Delta FCN\left(g-c-g\right)\)
\(\Rightarrow IN=CN\)
Xét tam giác vuông INF và tam giác vuông CNH có:
HN = FN
IN = CN
\(\Rightarrow\Delta INF=\Delta CNH\) (Hai cạnh góc vuông)
\(\Rightarrow\widehat{IFN}=\widehat{CHN}\)
Mà chúng lại ở vị trí so le trong nên IF // BC.
d) Chứng minh tương tự câu c, ta có IE // BC
Vậy thì qua I có hai tia IE và IF cùng song song với BC nên chúng trùng nhau.
Vậy I, E, F thẳng hàng.

a: Ta có: DB\(\perp\)AB
AC\(\perp\)AB
Do đó: DB//AC
Xét ΔECA có DB//AC
nên \(\dfrac{BE}{BA}=\dfrac{DE}{DC}\)
b: Xét ΔCEK có DB//EK
nên \(\dfrac{DB}{EK}=\dfrac{CD}{CE}\)(1)
Xét ΔAEI có DB//EI
nên \(\dfrac{DB}{EI}=\dfrac{AB}{AE}\left(2\right)\)
Ta có: \(\dfrac{BE}{BA}=\dfrac{DE}{DC}\)
=>\(\dfrac{BE+BA}{BA}=\dfrac{DE+DC}{DC}\)
=>\(\dfrac{AE}{BA}=\dfrac{CE}{DC}\)
=>\(\dfrac{CD}{CE}=\dfrac{AB}{AE}\left(3\right)\)
Từ (1),(2),(3) suy ra EI=EK

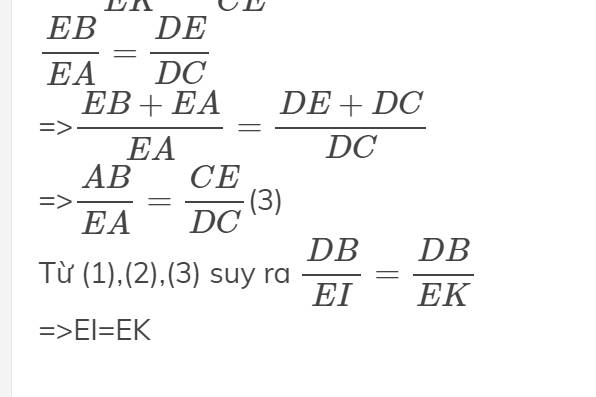
Đề không đầy đủ. Bạn xem lại nhé.