Question

[Thầy Cao Đô]

Bài 4. (2,5 điểm) Cho $\Delta { A B C}$ nhọn, đường cao $A H$. Kẻ $H E \perp {A B} \, (E \in A B), \, H F \perp {A C} \, (F \in A C)$.

a) Chứng minh $\Delta { A E H} \backsim \Delta { A H B}$ từ đó suy ra $A H^2=A E . A B$

b) Chứng minh $A E . A B=A F . A C$

c) Cho chu vi các $\Delta { A E F}$ và $\Delta { A C B}$ lần lượt là $20$ cm và $30$ cm. Tính diện tích $\Delta { A E F}$ và $\Delta { A C B}$ biết diện tích $\Delta { A C B}$ lớn hơn diện tích $\Delta { A E F}$ là $25$ cm$^2$.

Answer 1

[Kiều Vũ Linh]

  

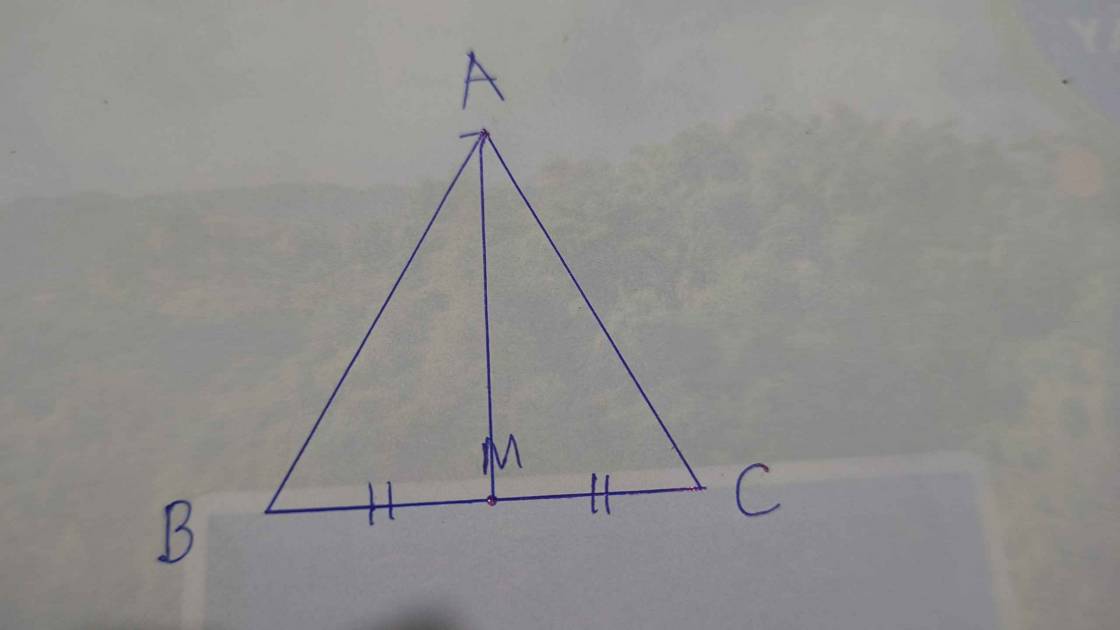
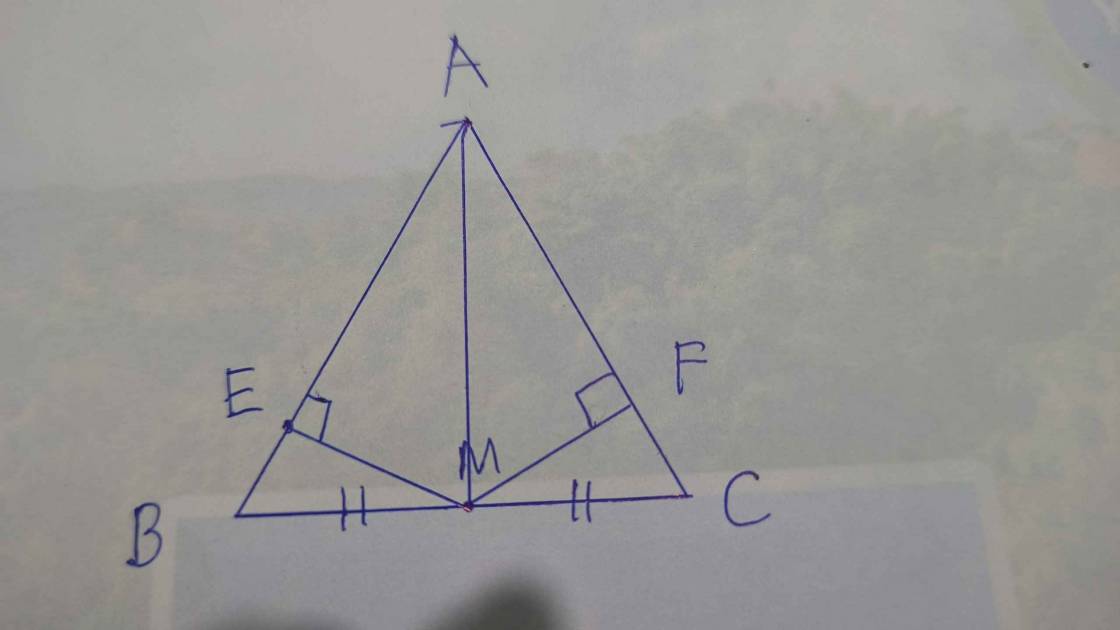
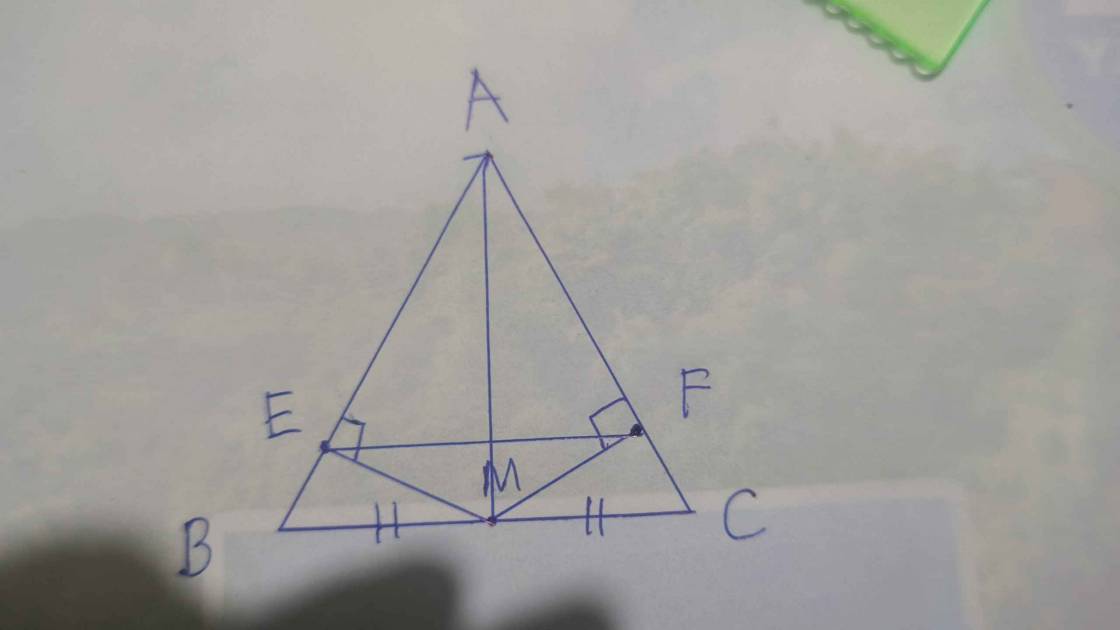
a) Xét hai tam giác vuông: ∆AEH và ∆AHB có:

∠A chung

⇒ ∆AEH ∽ ∆AHB (g-g)

⇒ AH/AB = AE/AH

⇒ AH² = AE.AB

b) Xét hai tam giác vuông: ∆AFH và ∆AHC có:

∠A chung

⇒ ∆AFH ∽ ∆AHC (g-g)

⇒ AH/AC = AF/AH

⇒ AH² = AF.AC

Mà AH² = AE.AB (cmt)

⇒ AE.AB = AF.AC

c) Do AE.AB = AF.AC (cmt)

⇒ AE/AC = AF/AB

Xét ∆AEF và ∆ACB có:

AE/AC = AF/AB (cmt)

∠A chung

⇒ ∆AEF ∽ ∆ACB (c-g-c)

Gọi p và p' lần lượt là chu vi của ∆AEF và ∆ACB

⇒ p/p' = 20/30= 2/3

Do ∆AEF ∽ ∆ACB (cmt)

⇒ AE/AC = AF/AB = EF/BC = p/p' = 2/3

Gọi x, y lần lượt là diện tích của ∆AEF và ∆ACB

Do ∆AEF ∽ ∆ACB (cmt)

⇒ x/y = (2/3)² = 4/9

⇒ x/4 = y/9

Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:

x/4 = y/9 = (y - x)/(9 - 4) = 25/5 = 5

x/4 = 5 ⇒ x = 5.4 = 20 (cm²)

y/9 = 5 ⇒ y = 5.9 = 45 (cm²)

Vậy diện tích ∆AEF là 20 cm², diện tích ∆ACB là 45 cm²

Answer 2

[Nguyễn Lê Phước Thịnh]