Phương trình √12x^2 -3x+4=3x +2 có tổng số nghiệm là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
N
1
CM
8 tháng 4 2017
Đáp án A
Phương trình 12 x + 4 - m . 3 x - m = 0 ⇔ 12 x + 4 . 3 x = m 3 x + 1 ⇔ m = 12 x + 4 . 3 x 3 x + 1 ( * ) .
Xét hàm số x f x = 12 x + 4 . 3 x 3 x + 1 trên khoảng (-1;0) có f ' x = 12 x . ( 3 x + 1 ) . ln 12 - ( 12 x - 4 ) . ln 3 3 x + 1 2 .
Ta có 12 x . 3 x + 1 . ln 12 - 12 x - 4 . ln 3 = 12 x . 3 x . ln 12 - ln 3 + 12 x . ln 2 + 4 . ln 3 > 0 ; ∀ x ∈ - 1 ; 0 .
Khi đó f ' x > 0 ; ∀ x ∈ - 1 ; 0 suy ra f(x) là hàm số đồng biến trên khoảng (-1;0)
Tính các giá trị f - 1 = 17 16 ; f 0 = 5 2 suy ra m i n f x = 17 16 và m a x f x = 5 2 .
Nên để phương trình (*) có nghiệm ⇔ m i n f ( x ) < m > m a x f x ⇒ m ∈ 17 16 ; 5 2 .
CM
11 tháng 8 2018
Đáp án A
Phương trình 12x + (4 – m).3x – m = 0 <=> 12x + 4.3x = m(3x + 1)
⇔ m = 12 x + 4 . 3 x 3 x + 1
Xét hàm số f x = 12 x + 4 . 3 x 3 x + 1 trên khoảng (–1;0) có
f ' x = 12 x . 3 x + 1 . ln 12 - 12 x - 4 . ln 3 3 x + 1 2
Ta có
12 x . 3 x + 1 . ln 12 - 12 x - 4 . ln 3 = 12 x . 3 x . ln 12 - ln 3 + 12 x . ln 2 + 4 . ln 3 > 0 ; ∀ x ∈ - 1 ; 0
Khi đó f’(x) > 0; ∀ x ∈ - 1 ; 0 suy ra f(x) là hàm số đồng biến trên khoảng (–1;0)
Tính các giá trị f - 1 = 17 16 ; f 0 = 5 2
⇒ m i n f x = 17 16 ; m a x f x = 5 2
Nên để phương trình (*) có nghiệm <=> min f(x) < m > max f(x)
⇒ m ∈ 17 6 ; 5 2
N
0
CM
27 tháng 8 2018
Đáp án B
Đặt t = 2x > 1
PT
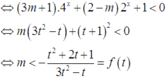
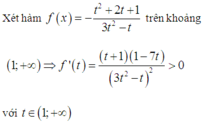
Dựa vào bảng biến thiên, suy ra m < -2
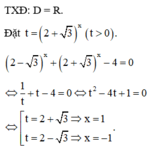
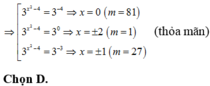
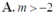
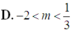
Bạn nên gõ đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề của bạn hơn nhé.