Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đầu tiên, ta cần tìm điểm cực trị của hàm số f(x) = x^3 - 3x^2 + m. Điều kiện cần và đủ để x_0 là điểm cực trị của hàm số y = f(x) là f’(x_0) = 0 và f’'(x_0) ≠ 0.
Ta có f’(x) = 3x^2 - 6x và f’'(x) = 6x - 6.
Giải phương trình f’(x) = 0, ta được x_1 = 0 và x_2 = 2. Kiểm tra điều kiện thứ hai, ta thấy f’‘(0) = -6 ≠ 0 và f’'(2) = 6 ≠ 0 nên x_1 = 0 và x_2 = 2 là hai điểm cực trị của hàm số.
Vậy, A = (0, f(0)) = (0, m) và B = (2, f(2)) = (2, 4 - m).
Trọng tâm G của tam giác OAB có tọa độ (x_G, y_G) = (1/3 * (x_A + x_B + x_O), 1/3 * (y_A + y_B + y_O)) = (2/3, 1/3 * (m + 4)).
Để G thuộc đường thẳng 3x + 3y - 8 = 0, ta cần có 3 * (2/3) + 3 * (1/3 * (m + 4)) - 8 = 0. Giải phương trình này, ta được m = 2.
Vậy, đáp án là B. m = 2.

Đáp án B
Đặt t = 2x > 1
PT
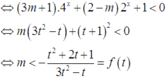
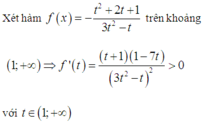
Dựa vào bảng biến thiên, suy ra m < -2

Ta có:
\(y'=x^2-2mx+m^2-4\)
\(y''=2x-2m,\forall x\in R\)
Để hàm số \(y=\dfrac{1}{3}x^3-mx^2+\left(m^2-4\right)x+3\) đạt cực đại tại x = 3 thì:
\(\left\{{}\begin{matrix}y'\left(3\right)=0\\y''\left(3\right)< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m^2-6m+5=0\\6-2m< 0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m=1,m=5\\m>3\end{matrix}\right.\Leftrightarrow m=5\)
=> B.

Đáp án: B.
Với m = 0, phương trình 2 x 3 - 5 = 0 có nghiệm duy nhất.
Với m ≠ 0, đồ thị hàm số y = 2 x 3 + 3m x 2 - 5 chỉ cắt Ox tại một điểm khi y CĐ . y CT > 0. Ta có y' = 6 x 2 + 6mx = 6x(x + m) = 0 có hai nghiệm là x = 0, x = -m; y(0) = -5, y(-m) = -2 m 3 + 3 m 3 - 5 = m 3 - 5.
Suy ra y(0).y(-m) = -5( m 3 - 5) > 0 ⇔ m < 5 3

\(\Delta'=m^2-8m+12\)
TH1: \(\Delta'< 0\Rightarrow\) phương trình có 2 nghiệm phức \(z_1;z_2\)
Do \(z_1=m-\sqrt[]{\Delta'};z_2=m+\sqrt{\Delta'}\Rightarrow z_1;z_2\) luôn luôn là 2 số phức liên hợp
\(\Rightarrow\left|z_1\right|=\left|z_2\right|\) luôn đúng khi \(m^2-8m+12< 0\)
\(\Rightarrow2< m< 6\Rightarrow m=\left\{3;4;5\right\}\)
TH2: \(\Delta'=0\Rightarrow m^2-8m+12=0\Rightarrow m=\left\{2;6\right\}\) pt có nghiệm kép (ktm)
TH3: \(\Delta'>0\Rightarrow\left[{}\begin{matrix}m>6\\m< 2\end{matrix}\right.\)
Pt có 2 nghiệm thực phân biệt, để \(\left|z_1\right|=\left|z_2\right|\Rightarrow\left[{}\begin{matrix}z_1=z_2\left(loại\right)\\z_1=-z_2\end{matrix}\right.\)
\(\Rightarrow z_1+z_2=0\Rightarrow2m=0\Rightarrow m=0\)
Vậy \(m=\left\{0;3;4;5\right\}\) có 4 giá trị nguyên của m

\(f^2\left(\left|x\right|\right)-\left(m-6\right)f\left(\left|x\right|\right)-m+5=0\) có \(a-b+c=0\) nên có các nghiệm \(\left[{}\begin{matrix}f\left(\left|x\right|\right)=-1\\f\left(\left|x\right|\right)=m-5\end{matrix}\right.\)
- Với \(f\left(\left|x\right|\right)=-1\Rightarrow\left|x\right|^2-4\left|x\right|+3=-1\Rightarrow\left|x\right|=2\Rightarrow x=\pm2\) có 2 nghiệm
- Xét \(f\left(\left|x\right|\right)=m-5\Leftrightarrow\left|x\right|^2-4\left|x\right|+8=m\) (1)
Từ BBT của \(y=\left|x\right|^2-4\left|x\right|+8\) dễ dàng suy ra (1) có 4 nghiệm pb khi \(4< m< 8\)
\(\Rightarrow m=\left\{5;6;7\right\}\) có 3 giá trị nguyên
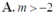
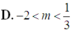

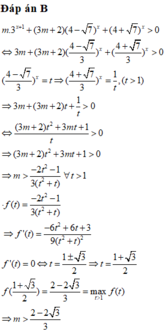

Đáp án A
Phương trình 12x + (4 – m).3x – m = 0 <=> 12x + 4.3x = m(3x + 1)
⇔ m = 12 x + 4 . 3 x 3 x + 1
Xét hàm số f x = 12 x + 4 . 3 x 3 x + 1 trên khoảng (–1;0) có
f ' x = 12 x . 3 x + 1 . ln 12 - 12 x - 4 . ln 3 3 x + 1 2
Ta có
12 x . 3 x + 1 . ln 12 - 12 x - 4 . ln 3 = 12 x . 3 x . ln 12 - ln 3 + 12 x . ln 2 + 4 . ln 3 > 0 ; ∀ x ∈ - 1 ; 0
Khi đó f’(x) > 0; ∀ x ∈ - 1 ; 0 suy ra f(x) là hàm số đồng biến trên khoảng (–1;0)
Tính các giá trị f - 1 = 17 16 ; f 0 = 5 2
⇒ m i n f x = 17 16 ; m a x f x = 5 2
Nên để phương trình (*) có nghiệm <=> min f(x) < m > max f(x)
⇒ m ∈ 17 6 ; 5 2