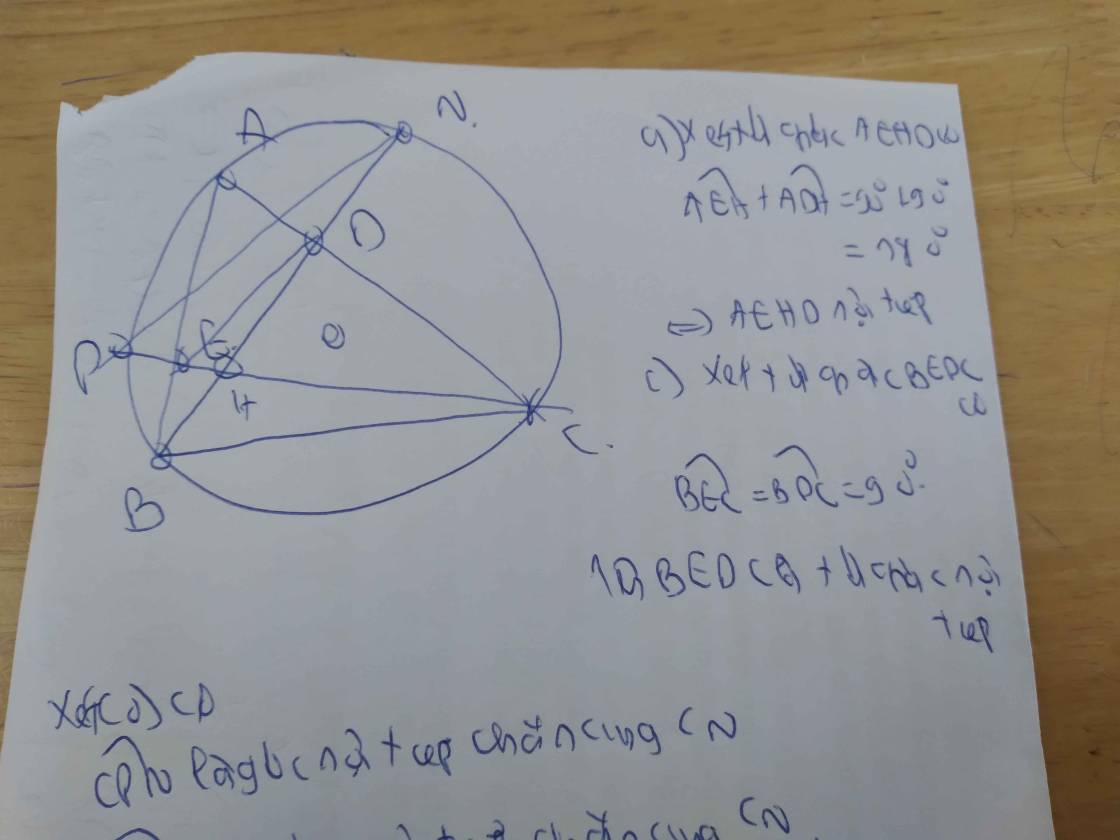
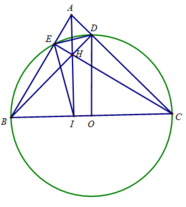
Cho tam giác ABC có ba góc nhọn (AB < AC) nội cao BD và CE cắt nhau tại H. b) Chứng minh EA .EB=EH.EC.
a) Chứng minh tứ giác AEHD là tứ giác nội tiếp. c) Gọi N và P lần lượt là giao điểm của BD và à CE với đường tròn (O). Chứng minh PN // ED. d) Gọi M là trung điểm của BC và F là giao điểm của AH với BC. Khi BC cố định, A chuyển động trên cung lớn BC. Chứng minh rằng đường tròn ngoại tiếp tam giác DEF luôn đi qua một điểm cố định.