Cho tam giác ABC có 3 cạnh lần lượt bằng a ,b,c .Chứng minh \(a^2=b^2+bc\Leftrightarrow\widehat{A}=2\widehat{B}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


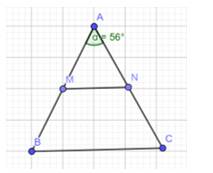
a) Theo đề bài ta có tam giác ABC cân ở A và \(\widehat A = {56^o}\)
Mà \( \Rightarrow \widehat A + \widehat B + \widehat C = {180^o}\)
\( \Rightarrow \widehat B = \widehat C = ({180^o} - {56^o}):2 = {62^o}\)
b) Vì tam giác ABC cân tại A nên AB = AC ( định nghĩa tam giác cân )
Mà M, N là trung điểm của AB, AC
Nên AM = AN
Xét tam giác AMN có AM = AN nên AMN là tam giác cân tại A
\( \Rightarrow \widehat M = \widehat N = ({180^o} - {56^o}):2 = {62^o}\)
c) Vì \(\widehat {AMN}=\widehat {ABC}\) (cùng bằng 62°)
Mà chúng ở vị trí đồng vị nên MN⫽BC


a ) AH là phân giác của \(\widehat{BAC}\)
\(\Rightarrow\widehat{EAH}=\widehat{FAH}\)
Xét 2 tam giác vuông ΔEAH và ΔFAH có:
AH chung
\(\widehat{EAH}=\widehat{FAH}\)
=> ΔEAH = ΔFAH (cạnh góc vuông - góc nhọn)
=> EH = FH (đpcm)
b ) \(\widehat{ACB}\) là góc ngoài tại C của ΔMCF
\(\Rightarrow\widehat{ACB}=\widehat{CFM}+\widehat{CMF}\)
\(\widehat{AEF}\) là góc ngoài tại E của ΔMBE
\(\Rightarrow\widehat{AEF}=\widehat{EMB}+\widehat{ABC}\)
Lại có : \(\widehat{CFM}=\widehat{AEF}\) (do ΔEAH = ΔFAH)
\(\Rightarrow\widehat{ACB}=\widehat{EMB}+\widehat{ABC}+\widehat{CMF}\)
Mặt khác \(\widehat{EMB}=\widehat{CMF}\) (đối đỉnh)
\(\Rightarrow\widehat{ACB}=2.\widehat{EMB}+\widehat{ABC}\)
Hay \(2.\widehat{BME}=\widehat{ACB}-\widehat{ABC}\)( ĐPCM )
c, ΔAHE vuông tại H
\(\Rightarrow HE^2+AH^2=AE^2\)
ΔEAH = ΔFAH ⇒ HE = HF => H là trung điểm của FE
\(\Rightarrow HE=\frac{FE}{2}\)
\(\Rightarrow HE^2=\left(\frac{FE}{2}\right)^2=\frac{FE^2}{4}\)
\(\Rightarrow\frac{FE^2}{4}+AH^2=AE^2\left(đpcm\right)\)
, Qua C kẻ đường thẳng song song với AB cắt EF ở D.
CD ║ AB \(\Rightarrow\widehat{CDF}=\widehat{AEH}\) (đồng vị)
mà \(\widehat{AFH\:}=\widehat{AEH}\)(ΔEAH = ΔFAH)
\(\Rightarrow\widehat{CDF}=\widehat{AFH\:}\)
=> ΔCDF cân tại C
=> CD = CF
Dễ dàng chứng minh được ΔMBE = ΔMCD (g.c.g)
⇒ BE = CD mà CD = CF
⇒ BE = CF (đpcm)

Trên tia đối của $MA$ lấy $N$ sao cho $MN=MA$
Ta có:
$BM=CM(gt)$
$\widehat{AMB}=\widehat{NMC}(đđ)$
$MA=MN(gt)$
$\Rightarrow \Delta{MAB}=\Delta{MNC}(c.g.c)$
$\Rightarrow AB=NC$ và $\widehat{MBA}=\widehat{MCN}$
Do đó $\widehat{MBA}=\widehat{MCN}$ nên $AB||NC$
$\Rightarrow \widehat{BAC}+\widehat{ACN}=90^o$
Lại có: $\widehat{BAC}=90^o$ nên $\widehat{ACN}=90^o$
$\Rightarrow \Delta{ABC}=\Delta{CNA}(c-g-c)$ vì:
$AC:chung$
$\widehat{BAC}=\widehat{ACN}=90^o$
$AB=NC$
$\Rightarrow BC=AN$
$\Rightarrow AM=\dfrac{1}{2}BC$ (đpcm)

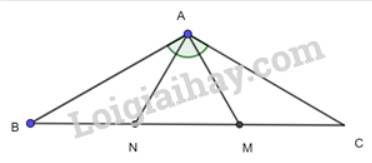
a) Xét 2 tam giác vuông BAM và CAN có:
\(\widehat{BAM} = \widehat{CAM}(=90^0)\)
AB=AC (Do tam giác ABC cân tại A)
\(\widehat B = \widehat C\) (Do tam giác ABC cân tại A)
=>\(\Delta BAM = \Delta CAN\)(g.c.g)
b) Cách 1:
Xét tam giác ABC cân tại A, có \(\widehat {A{\rm{ }}} = 120^\circ \) có:
\(\widehat B = \widehat C = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\).
Xét tam giác ABM vuông tại A có:
\(\widehat {B} + \widehat {BAM} + \widehat {AMB} = {180^o}\\ \Rightarrow {30^o} + {90^o} + \widehat {AMB} = {180^o}\\ \Rightarrow \widehat {AMB} = {60^o}\\ \Rightarrow \widehat {AMC} = {180^o} - \widehat {AMB} = {180^o} - {60^o} = {120^o}\)
Xét tam giác MAC có:
\(\begin{array}{l}\widehat {AMC} + \widehat {MAC} + \widehat C = {180^o}\\ \Rightarrow {120^o} + \widehat {MAC} + {30^o} = {180^o}\\ \Rightarrow \widehat {MAC} = {30^o} = \widehat C\end{array}\)
\(\Rightarrow \) Tam giác AMC cân tại M.
Vì \(\Delta BAM = \Delta CAN\)
=> BM=CN ( 2 cạnh tương ứng)
=> BM+MN=CN+NM
=> BN=CM
Xét 2 tam giác ANB và AMC có:
AB=AC (cmt)
\(AN = AM\)(do \(\Delta BAM = \Delta CAN\))
BN=MC (cmt)
=>\(\Delta ANB = \Delta AMC\)(c.c.c)
Mà tam giác AMC cân tại M.
=> Tam giác ANB cân tại N.
Cách 2:
Xét tam giác ABC cân tại A, có \(\widehat {A{\rm{ }}} = 120^\circ \) có:
\(\widehat B = \widehat C = \frac{{{{180}^o} - {{120}^o}}}{2} = {30^o}\).
Xét tam giác ABM vuông tại A có:
\(\widehat B + \widehat {BAM} + \widehat {AMB} = {180^o}\\ \Rightarrow {30^o} + {90^o} + \widehat {AMB} = {180^o}\\ \Rightarrow \widehat {AMB} = {60^o}\)
Vì \(\Delta BAM = \Delta CAN\) nên AM = AN (2 cạnh tương ứng)
=> \(\Delta AMN\) đều (Tam giác cân có 1 góc bằng 60 độ)
=> \(\widehat {NAM}=60^0\)
Ta có: \(\widehat{BAN}+\widehat{NAM}=\widehat{BAM}\)
=> \(\widehat{BAN} + 60^0=90^0\)
=> \(\widehat{BAN}=30^0\)
Xét tam giác ABN có \(\widehat{BAN}=\widehat{ABN}(=30^0\) nên \(\Delta ABN\) cân tại N.
Ta có: \(\widehat{CAM}+\widehat{NAM}=\widehat{CAN}\)
=> \(\widehat{CAM} + 60^0=90^0\)
=> \(\widehat{CAM}=30^0\)
Xét tam giác ACM có \(\widehat{CAM}=\widehat{ACM}(=30^0\) nên \(\Delta ACM\) cân tại M.