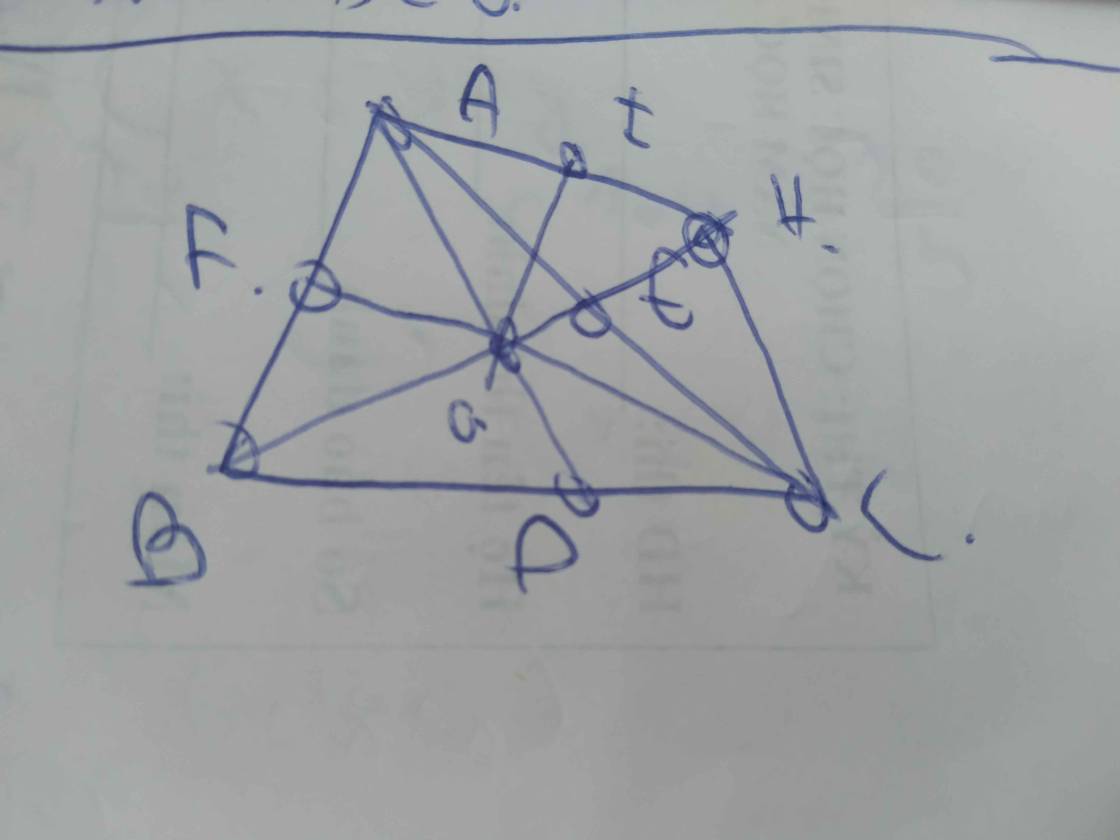
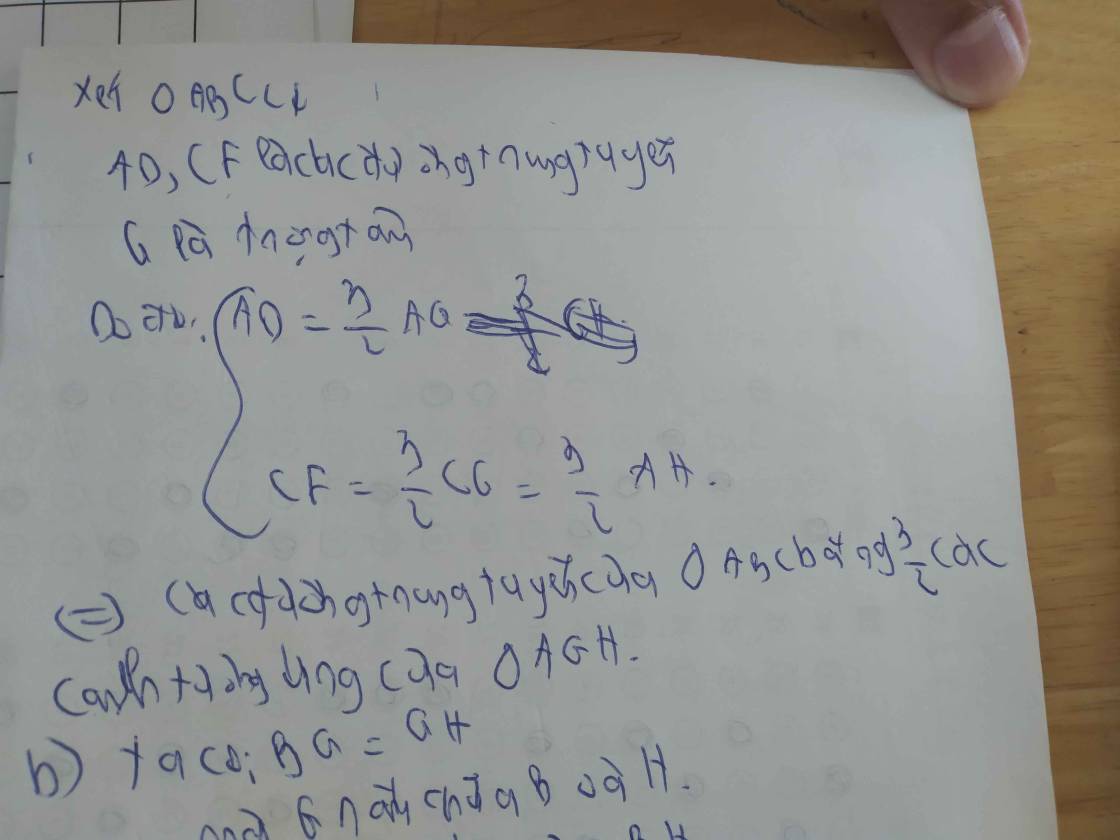Cho hình tam giác ABC có các đường trung tuyến AD, BE, CF cắt nhau tại G. Trên tia đối của EB, lấy H sao cho EG = EH. Gọi I là trung điểm của AH. Chứng minh rằng:
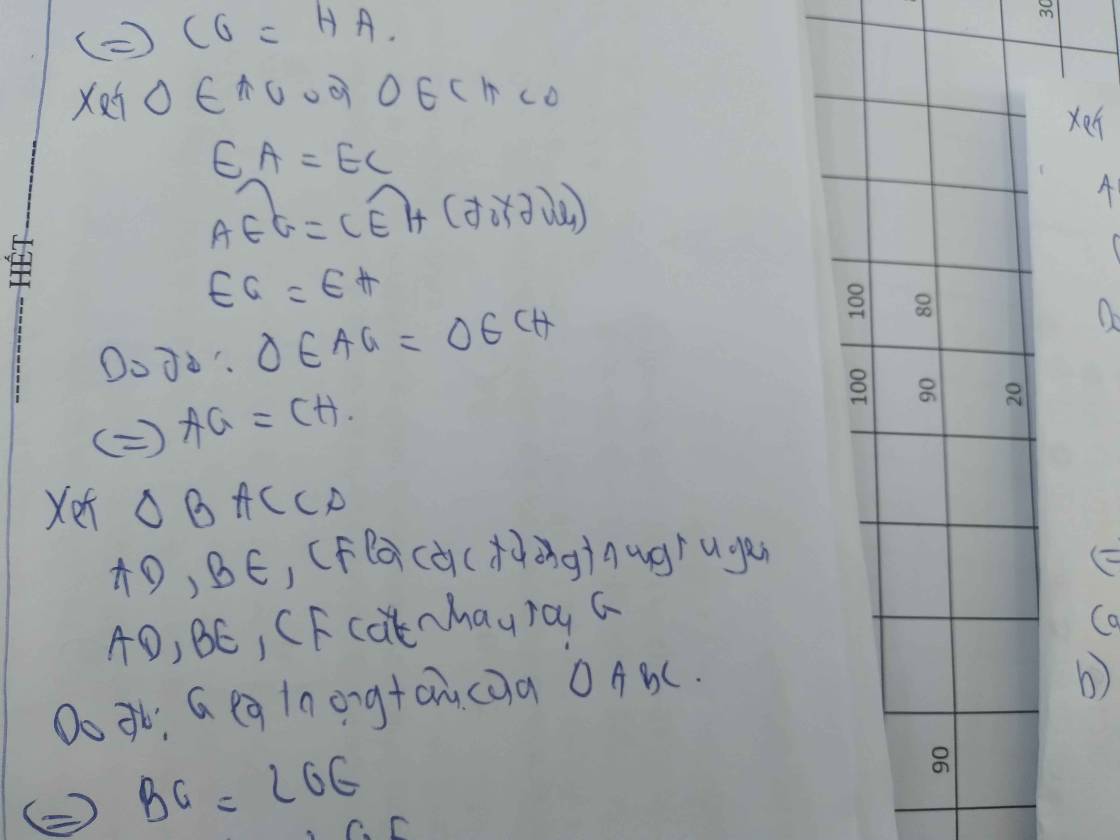
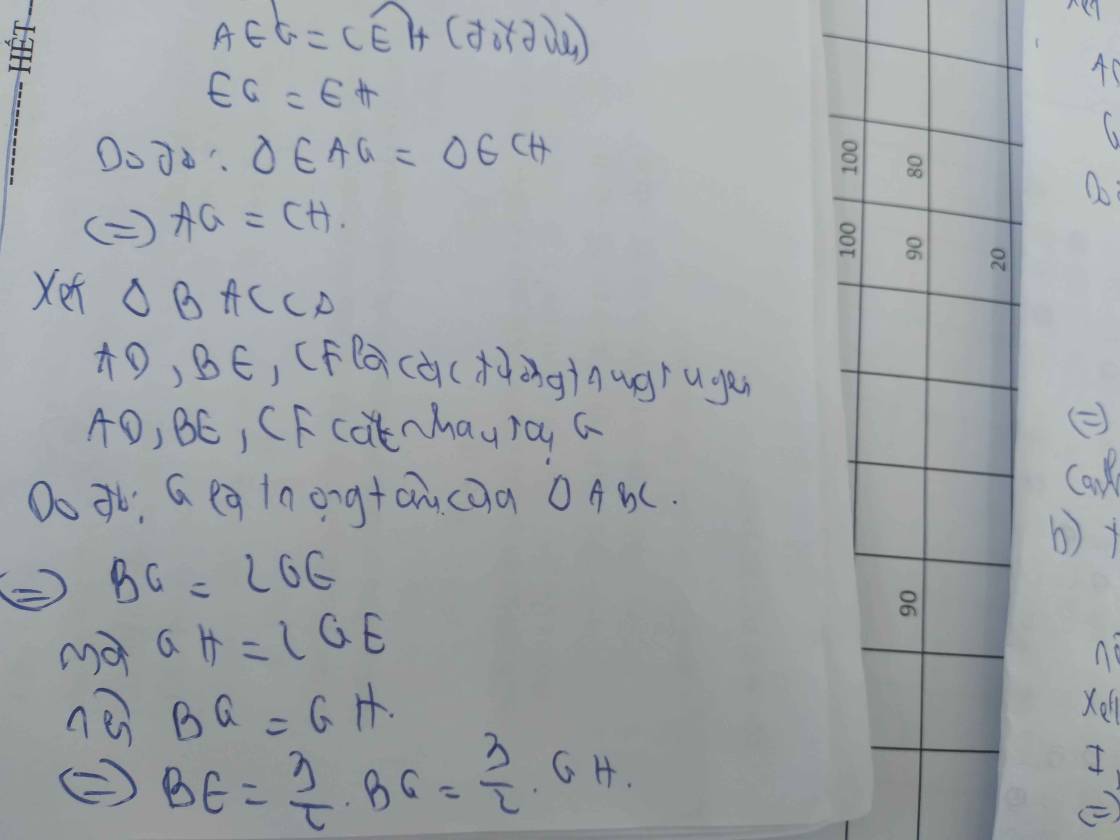
a, Các đường trung tuyến của tam giác ABC bằng 3/2 các cạnh của tam giác AGH
b, IG = AF
GIÚP MÌNH VỚI Ạ