Cho đường tròn tâm O dây cung AB điểm M di chuyển trên cung lớn AB các đường cao AE, BF của đường tam giác ABM cắt nhau tại H. Đường tròn tâm H bán kính HM cắt MA, MB theo thứ tự của C, D.
a) chứng minh rằng đường thẳng kẻ từ M vuông góc với CD luôn đi qua một điểm cố định
b) chứng minh rằng đường thẳng kẻ từ H vuông góc với CD cũng đi qua một điểm cố định
MN GIÚP MIK VỚI...
Đọc tiếp
Cho đường tròn tâm O dây cung AB điểm M di chuyển trên cung lớn AB các đường cao AE, BF của đường tam giác ABM cắt nhau tại H. Đường tròn tâm H bán kính HM cắt MA, MB theo thứ tự của C, D.
a) chứng minh rằng đường thẳng kẻ từ M vuông góc với CD luôn đi qua một điểm cố định
b) chứng minh rằng đường thẳng kẻ từ H vuông góc với CD cũng đi qua một điểm cố định
MN GIÚP MIK VỚI Ạ
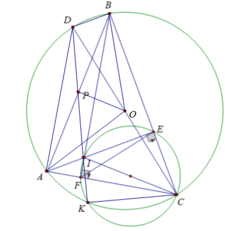
a) Kẻ tiếp tuyến Mx của (O). Khi đó \(Mx\perp MO\).
Ta thấy \(\widehat{xMA}=\widehat{MBA}=\widehat{MFE}\) nên Mx // EF. Do đó \(EF\perp MO\)
Mặt khác, tam giác HAC cân tại H có đường cao HF nên F là trung điểm MC. Tương tự, E là trung điểm MD. Vì vậy, EF là đường trung bình của tam giác MCD \(\Rightarrow\) EF//CD.
Do đó, \(MO\perp CD\) \(\Rightarrow\) đt qua M vuông góc với CD đi qua O cố định.
b) Gọi O' là điểm đối xứng của O qua AB. Kẻ đường kính MK của (O), gọi P là trung điểm AB. Lúc này O' là điểm cố định.
Khi đó AH//BK (cùng vuông góc với MB) và BH//AK (cùng vuông góc với MA) nên tứ giác AHBK là hình bình hành
\(\Rightarrow\) Trung điểm P của AB cũng là trung điểm của HK.
\(\Rightarrow\) OP là đường trung bình của tam giác KMH
\(\Rightarrow\) OP//MH và \(OP=\dfrac{1}{2}MH\)
\(\Rightarrow\) OO'//MH và \(OO'=MH\)
\(\Rightarrow\) Tứ giác MOO'H là hình bình hành
\(\Rightarrow\) HO' // MO
Mà \(MO\perp CD\) (cmt) nên \(HO'\perp CD\)
Như vậy đường thẳng qua H và vuông góc với CD đi qua O' cố định.