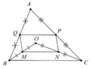
Tam giác ABC, hình chữ nhật MNPQ nội tiếp tam giác sao cho M,N \(\in\)BC, P\(\in\)AC, Q\(\in\)AB.
a) CMR: Tâm hình chữ nhật MNPQ luôn nằm trên một đường thẳng cố định khi MNPQ thay đổi.
b) Xác định vị trí của P để diện tích MNPQ max
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lỗi nên không vẽ được hình nha bạn !!!
Bài giải
Gọi E,F , R , S theo thứ tự là trung điểm của đường cao AH ,cạnh BC ,MQ ,NP.Gọi O là trung điểm của RS .Dùng bổ đề hình thang chứng minh B,R,E thẳng hàng ,C,S,E thẳng hàng ,E , O ,F thẳng hàng .Điểm O chuyển động trên đoạn thẳng EF, trừ E và F .

Vì ∆ ABC đồng dạng với ∆ AMN nên:
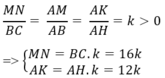
Diện tích hình chữ nhật MNPQ là:
SMNPQ = MN. NP = MN.KH = MN.( AH – AK)
=> SMNPQ = 16k.( 12- 12k)
Theo đề bài diện tích hình chữ nhật đó là 36cm2 nên
16k.( 12- 12k ) = 36
⇔ 16k.12( 1- k) = 36
⇔ 16k(1 – k) = 3 ( chia cả hai vế cho 12)
⇔ 16k – 16k2 = 3
⇔ 16k2- 16k + 3= 0
Ta có: ∆’= (-8)2 – 16.3 = 16> 0
Phương trình trên có 2 nghiệm là:
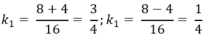
Vậy để diện tích hình chữ nhật MNPQ là 36cm2 thì vị trí điểm M phải thỏa mãn:
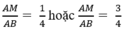

Vì ∆ ABC đồng dạng với ∆ AMN nên:
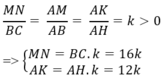
Diện tích hình chữ nhật MNPQ là:
SMNPQ = MN. NP = MN.KH = MN.( AH – AK)
=> SMNPQ = 16k.( 12- 12k)
Theo đề bài diện tích hình chữ nhật đó là 36cm2 nên
16k.( 12- 12k ) = 36
⇔ 16k.12( 1- k) = 36
⇔ 16k(1 – k) = 3 ( chia cả hai vế cho 12)
⇔ 16k – 16k2 = 3
⇔ 16k2- 16k + 3= 0
Ta có: ∆’= (-8)2 – 16.3 = 16> 0
Phương trình trên có 2 nghiệm là:
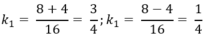
Vậy để diện tích hình chữ nhật MNPQ là 36cm2 thì vị trí điểm M phải thỏa mãn:
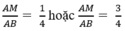

a) HS tự chứng minh
b) O nằm trên đường cao xuất phát từ đỉnh A của DABC
vào câu hỏi tương tự
Bui Duc Viet tham khảo nhé
Gọi diện tích h.c.n MNPQ là S1, diện tích tam giác ABC là S2=a
Ta có S1/S2 = PQ.QM//AH.BC (*)
Do PQ//BC => PQ/BC=AQ/AB
Do QM//AH => QM/AH=BQ/AB
(*) => S1/S2 = AQ.BQ/AB^2
=> S1=a.AQ.BQ/AB^2
=> S1 lớn nhất khi AQ.BQ lớn nhất
Ta có AQ.BQ<= [(AQ+BQ)/2]^2=(AB/2)^2
AQ.BQ lớn nhất khi AQ=BQ
=> Diện tích hình chữ nhật MNPQ có giá trị lớn nhất khi PQ đi qua trung điểm của đường cao AH.